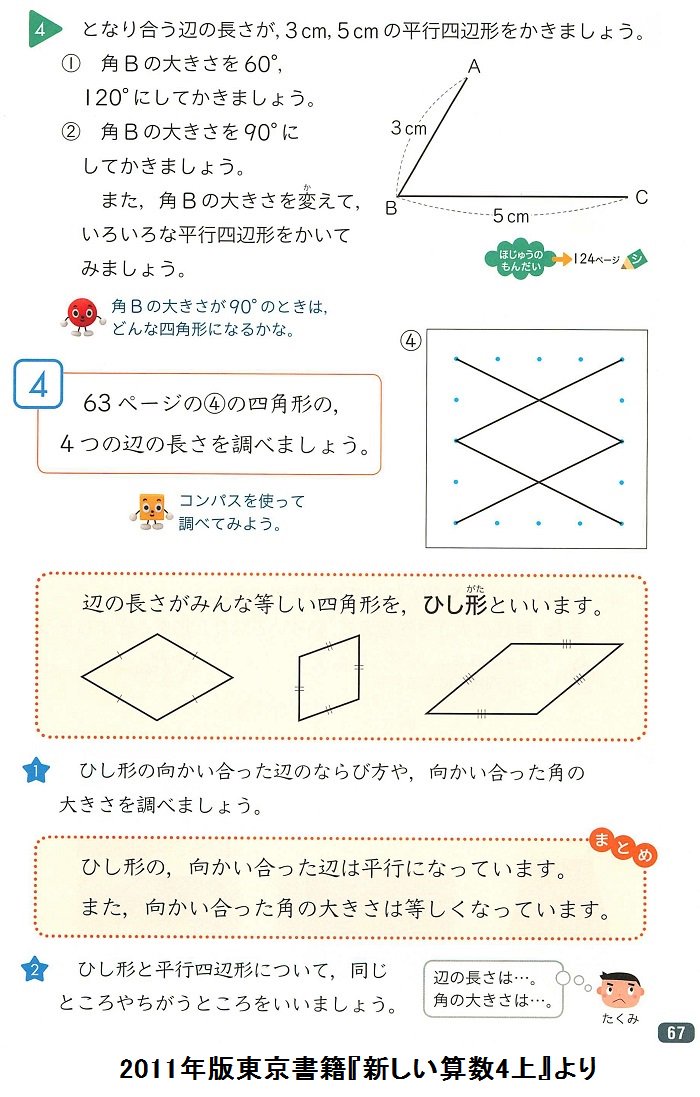
3 特別な平行四辺形 4 面積が等しい三角形 数学 1 式の計算 1 単項式と多項式 数学 1 式の計算 2 多項式の計算 数学 平行四辺形の性質と長さや角度を求める問題です。 平行四辺形の性質は小学校で習ったものと同じですが、証明で使えるように定義、性質、条件などを自分で説明できるようにしっかり理解するようにしてください。 特別な四角形の定義 ひし形→4つの 対辺・対角定義対辺:四角形の向かい合う辺対角:四角形の向かい合う角平行四辺形定義平行四辺形:2組の対辺がそれぞれ平行な四角形平行四辺形の定理定理平行四辺形の性質 2組の対辺はそれぞれ等しい 2組の対角はそれぞれ等しい 2つの対角
特別な平行四辺形1
特別な平行四辺形 問題 中2
特別な平行四辺形 問題 中2- 『特別な平行四辺形 さわってうごく数学「aquaアクア」』の評価とレビュー 『特別な平行四辺形 さわってうごく数学「aquaアクア」』の最新アップデート情報 14年10月30日 バージョン0 いくつかのバグ修正。 メモ機能の追加。三角形は全部で5種類あります。 四角形はどうでしょうか。 四角形 のほかに特別な四角形として、 台形 ・ 平行四辺形 ・ ひし形 ・ 長方形 ・ 正方形




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
四角形の分類 09年6月1日 15年4月6日 ototo219 数学 図が小さいかと思いますが、クリックすると大きくなりますので、図を見ながらお読みください。 正方形、長方形、平行四辺形、、、と小学校から特別な性質を持つ四角形というのが 登場します「3、特別な平行四辺形」 教科書が出ているか確認する。 教師が範読。 「長方形の定義は 4つの角がすべて直角である四角形 である」 教科書を出していない生徒に、教科書コピーを渡す。 私語をしている生徒そばに行き、教科書の場所を指さす。⑤ 特別な平行四辺形 平行四辺形5条件に、さらに厳しい条件を加えると 「長方形」や「ひし形」や「正方形」になりますね! 「付け加える」ということは、これら3つの図形は それぞれ「平行四辺形の条件」を全て備えているということですね (1) 長方形
《特別な平行四辺形》 長方形の4つの角はすべて等しい 2組の対角がそれぞれ等しい a b c d したがって、長方形は平行四辺形式による説明 (3) 式の計算 総合問題1 5 連立文章題 (速さ3) (2) 二等辺三角形2 2 平行四辺形折り返し1 2 三角形証明 (発展2) 2 三角形証明 (発展1) 3 平行四辺形の性質の利用3 1 三角形証明 (発展3) 3 「平行四辺形」の4つの角が直角になると「長方形」に なります。 ひし形は平行四辺形の特殊な形であるといえます。 ですから「ひし形を平行四辺形に分類」はあながち間違えではないです。 そうであれば「長方形を平行四辺形に分類」でもいいですよね。
長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する第17巻 特別な平行四辺形・等積変形の本質DVDの内容 ① 長方形とは、 定義 4つの角が等しい四角形。 定理 長方形の2つの対角線の長さは、等しい。 この定理を証明します。 ② ひし形とは、 定義 4つの辺が等しい四角形。 定理 ひし形の対角線は、垂直に 正方形、長方形、ひし形が平行四辺形に含まれる というのは、中学生になってから受ける説明です。 そして、長方形やひし形を『平行四辺形の特別な場合』 正方形を『長方形とひし形の両方の性質をもつ』 としていました。 小学生のうちは、それらを




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
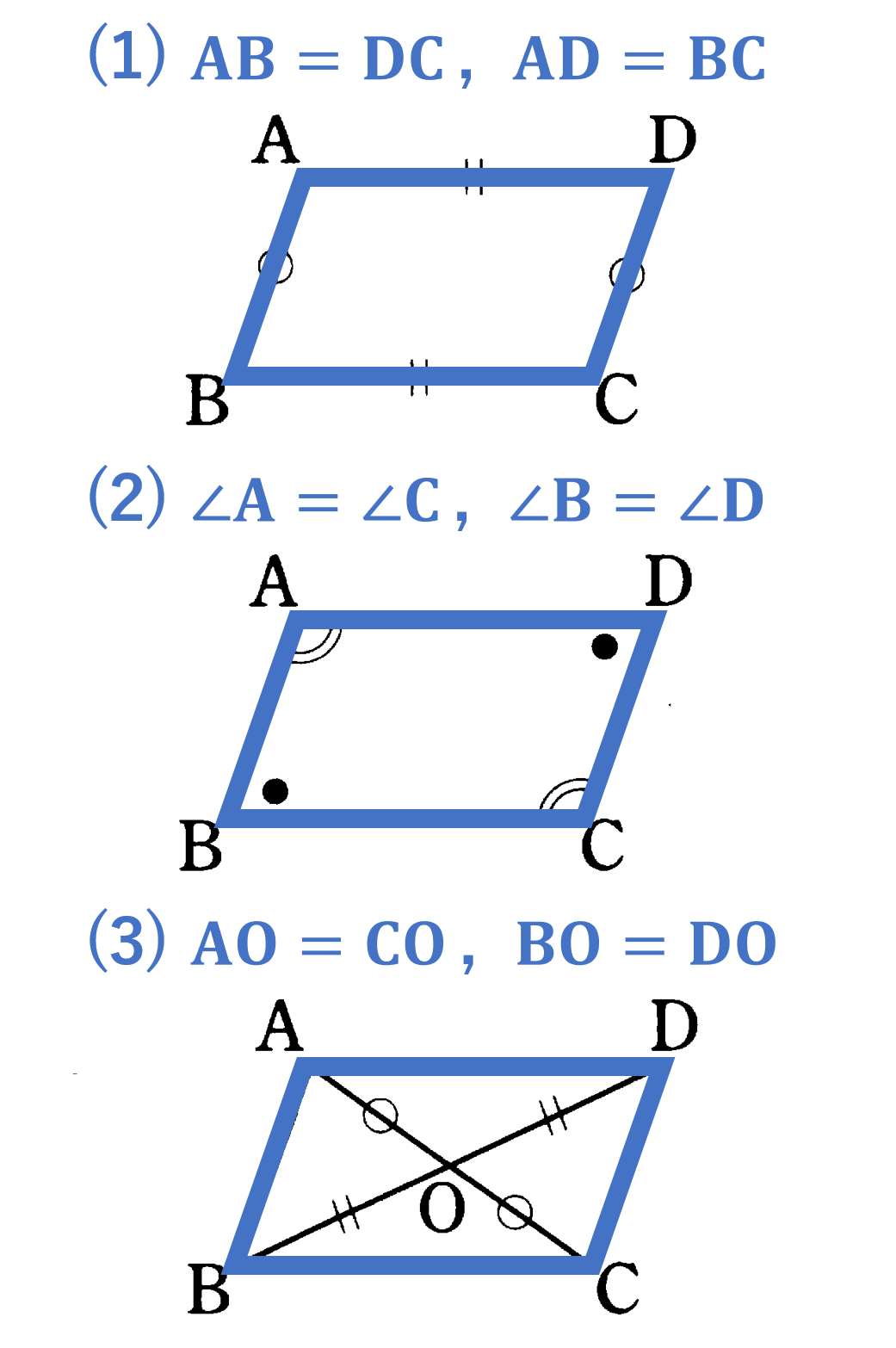
特別な平行四辺形(長方形、ひし形、正方形)であることを証明しようと思ったら写真の 1、 2、 3のどれを証明に使ってもいいんですか?それとも使っていいのは 3だけでしょうか? 平行四辺形の条件 ある平面図形が平行四辺形であるための条件には、次の \(5\) つがあります。 このうちどれか \(1\) つでも条件を満たせば、その図形は平行四辺形と言えます。 条件①2 組の向かい合う辺が平行である これは平行四辺形の定義と同じ平行四辺形が長方形になる3つの条件,平行四辺形がひし形になる3つの条件をもとに考えます (№19参照)。 *6種類の四角形のそれぞれがもつ個々の性質を個別に覚えてもすぐに忘れます。 №15で学習したように,四角形から正方形までの四角形の特殊化
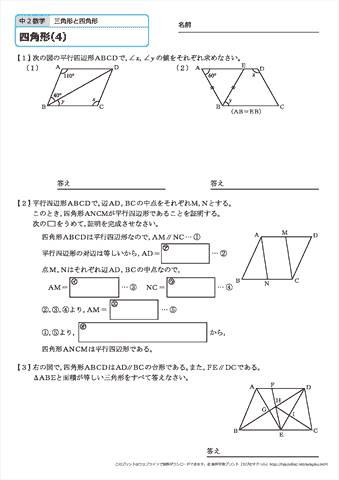



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平行四辺形の仲間を知ろう 電験3種web
会員専用ページ都麦出版・つむぎ出版 都麦出版TOPページ > 会員専用ページ ステップ式数学 教師用マニュアル 1 PDF ZIP Ⅰ 正負の数 1.正の数・負の数 正負の数 平行四辺形とは、「 2組の向かい合う辺(対辺)が、それぞれ平行な四角形 」のことを指します。 また、平行四辺形は 台形 の一種です。 さらに、平行四辺形の中には特別に名前のついている四角形があり、それが 正方形やひし形、長方形 と呼ばれる四角形さらに,「四角形」から「台形」「平行四辺形」と特別な形になるほど,その性質が増えていくことから相互関係に目を向けるようにしたいと考えている。 3.指導計画(14時間) 第1次 播磨町や校区の地図から垂直・平行を考える。(5時間)



Ed City Daito Osaka Jp



1
ひし形abcdは平行四辺形である。 まとめ 長方形やひし形や正方形は平行四辺形の仲間である。 長方形やひし形の対角線の性質を調べます。特別な平行四辺形 長方形、ひし形、正方形はすべて平行四辺形の一種であり、平行四辺形の性質をすべてもっています。 その中でも正方形は、長方形とひし形の性質をもつ、平行四辺形の中でも王様のような図形です。 どの図形がどんな性質を持っている・ 長方形、ひし形、正方形には、平行四辺形の性質があることに関心をもち、それぞれ の性質についてまとめようとする。 ・ 長方形、ひし形、正方形が平行四辺形の特別な場合であるとみることができ




中学2年数学 平行四辺形の性質 練習問題5 あんのん塾




中学数学 特別な平行四辺形について Clearnote
特別な平行四辺形 長方形、ひし形、正方形はすべて平行四辺形の一種であり、平行四辺形の性質をすべてもっています。 その中でも正方形は、長方形とひし形の性質をもつ、平行四辺形の中でも王様のような図形です。 どの図形がどんな性質を持っている三角形・四角形 二等辺三角形の性質(1) 問題一括 (4,155Kb) 解答一括 (4,859Kb) 二等辺三角形の性質(2) 二等辺三角形の性質(3) 2つの正三角形 二等辺三角形になるための条件(1) 二等辺三角形になるための条件(2) 定理の逆 直角三角形の合同(1) 直角三角形の合同(2)今回は、 「特別な平行四辺形」 について学習するよ。 「特別な平行四辺形」とは、 「長方形」 、 「ひし形」 、 「正方形」 の3つことなんだ。



5章2節05 特別な平行四辺形 中村 翔
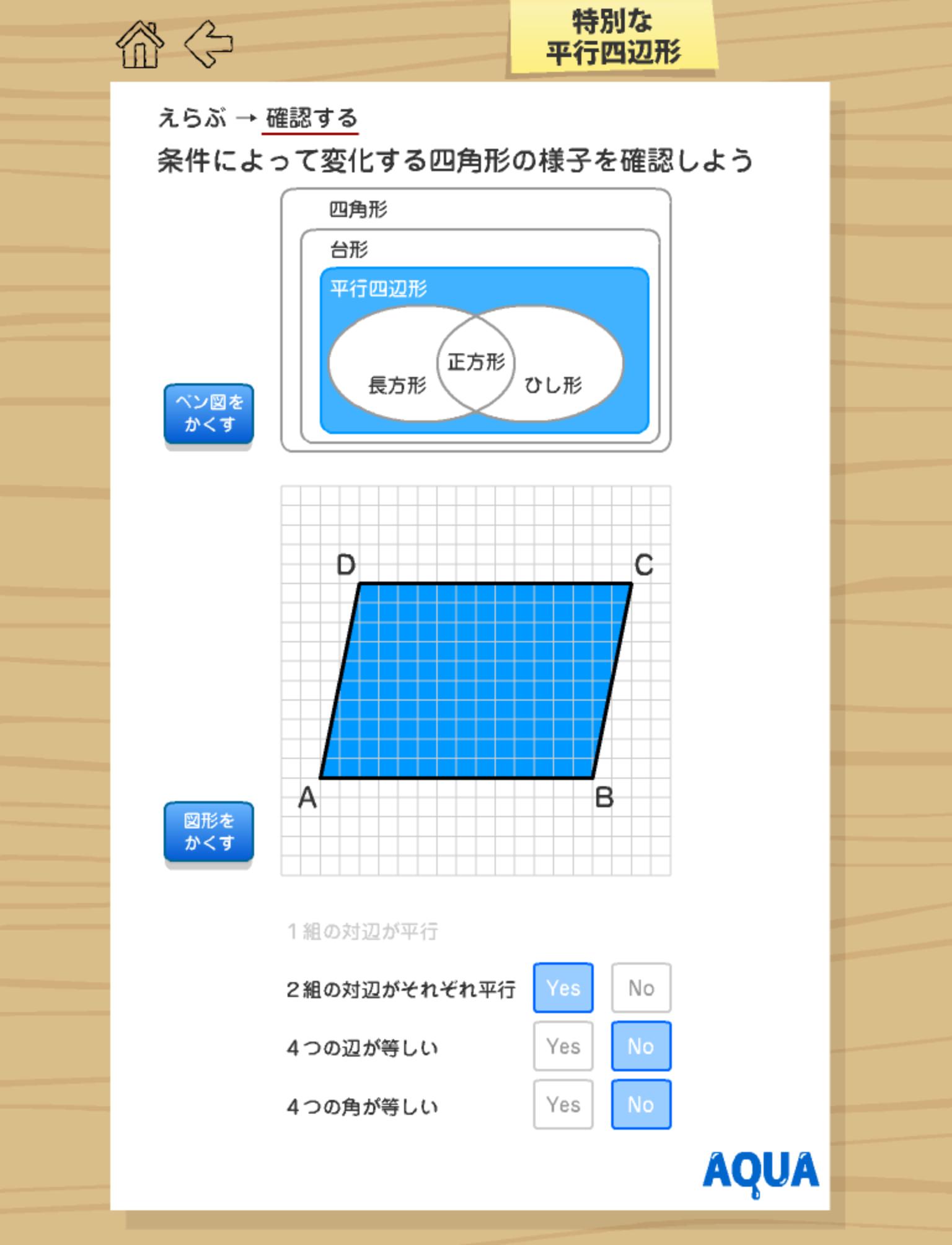



特別な平行四辺形 さわってうごく数学 Aquaアクア For Android Apk Download
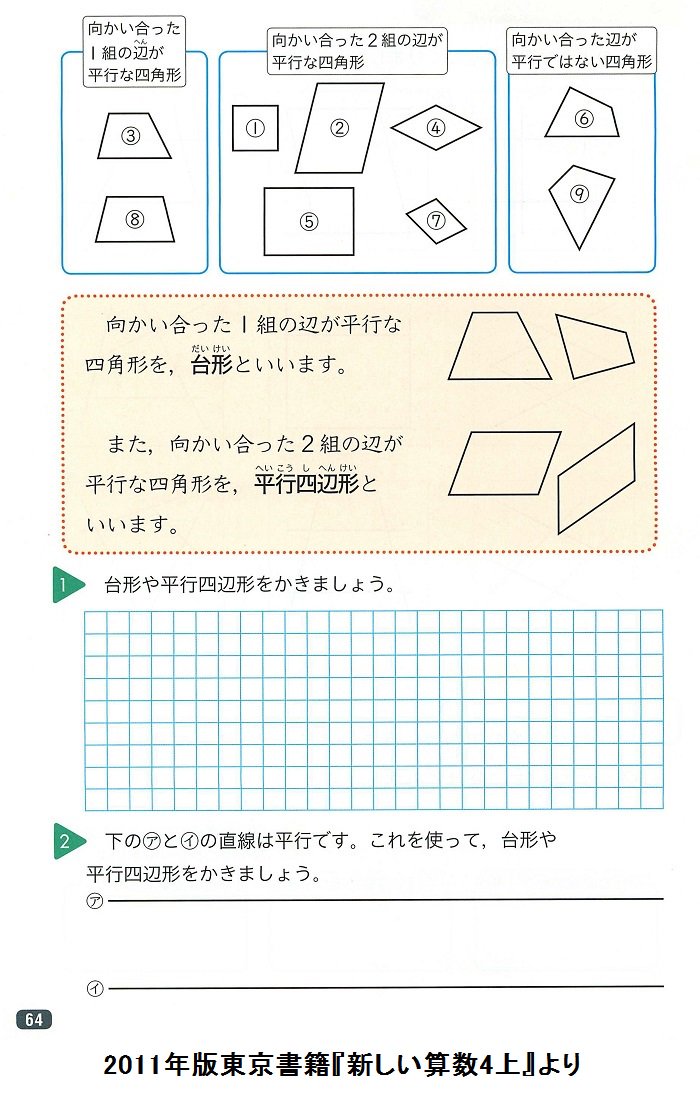



黒木玄 Gen Kuroki V Twitter 掛算 訂正後の主張 拡散すべき情報はこのツイートに再掲する添付画像だと思います 平行四辺形が 特別な場合として 長方形 正方形 ひし形を含むことが明瞭な説明になっているのに 台形が平行四辺形を含むという説明になっていません



特別な平行四辺形1



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形




中学2数学 20 特別な平行四辺形の証明 2 Youtube



至急です 特別な平行四辺形 証明 Yahoo 知恵袋




Math 平行四辺形 平行四辺形になることの証明 働きアリ
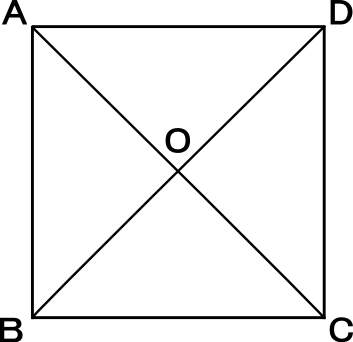



中学2年数学練習問題 平行四辺形 長方形 ひし形 正方形 の性質
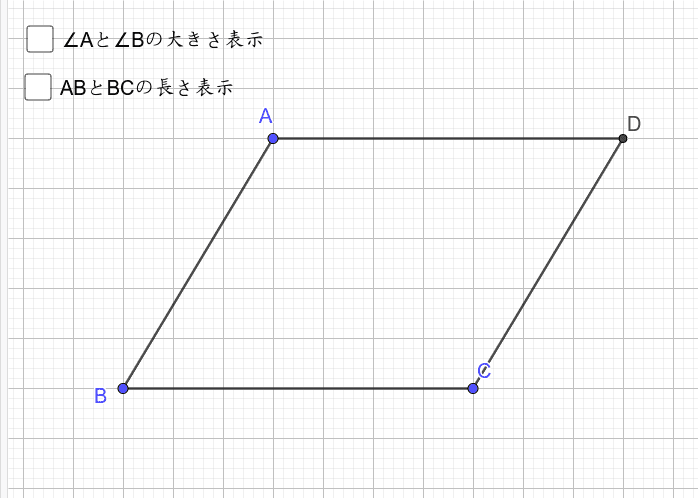



中2 平行四辺形 特別な平行四辺形 Geogebra




高校受験入試で頻出 特別な三角形 四角形の定義とその証明
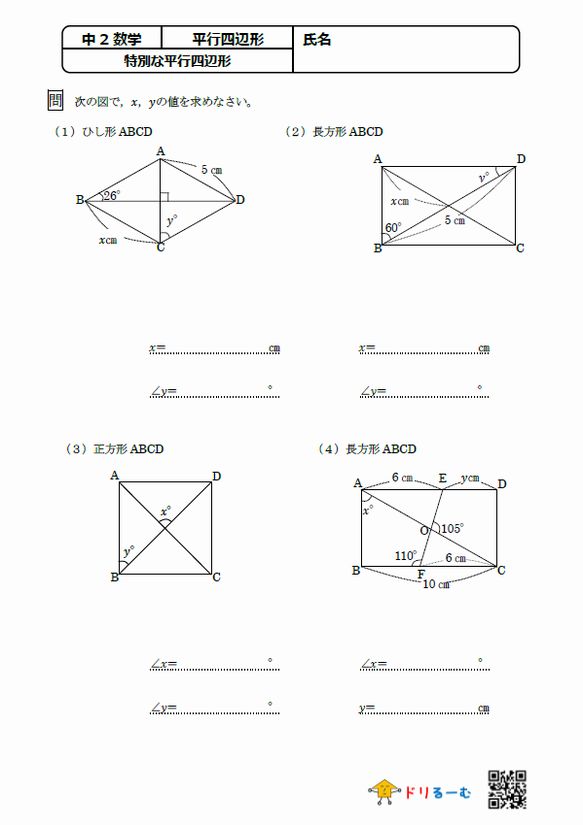



特別な平行四辺形 ドリるーむ




中学2年生数学 特別な平行四辺形 についてのまとめ 我流舎ウェブかわら版 川西市山下 個別指導塾 我流舎のブログ




中学校2年生数学 特別な平行四辺形 平行線と面積




中2 特別な平行四辺形 平行線と面積 中学生 数学のノート Clearnote




図形と証明 特別な平行四辺形 Youtube



特別な平行四辺形 等積変形の本質 高校受験合格法




楽しい講義 中2数学 特別な平行四辺形 平行線と面積2 連問1 Youtube



特別な平行四辺形2




無料 中2数学 基本問題 問題プリント 232 平行四辺形3 長方形とひし形
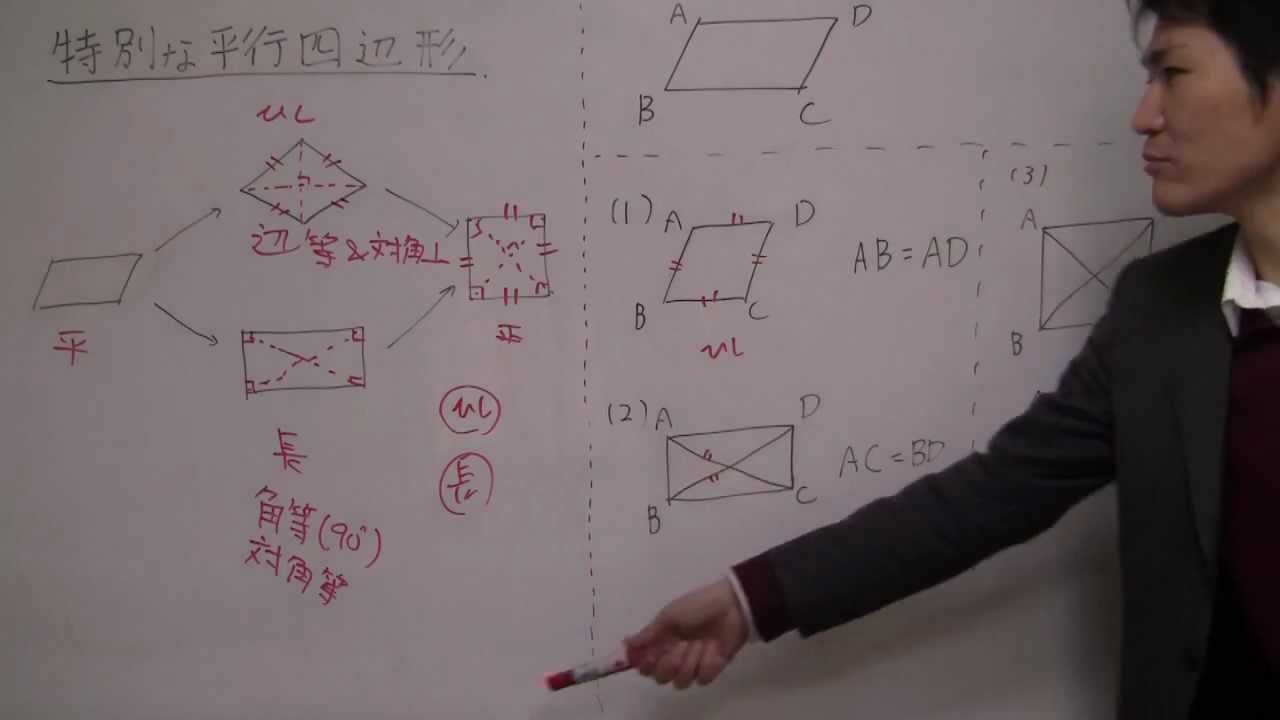



中学2数学 20 特別な平行四辺形 ひし形 長方形 正方形 1 Youtube



3




中2 数学 特別な平行四辺形 中学生 数学のノート Clearnote




中2数学 長方形 ひし形 正方形 映像授業のtry It トライイット




中2数学 特別な平行四辺形145 147 中間期末テスト用 赤城 ᐡᐤᐡ



Tsumugi Ne Jp
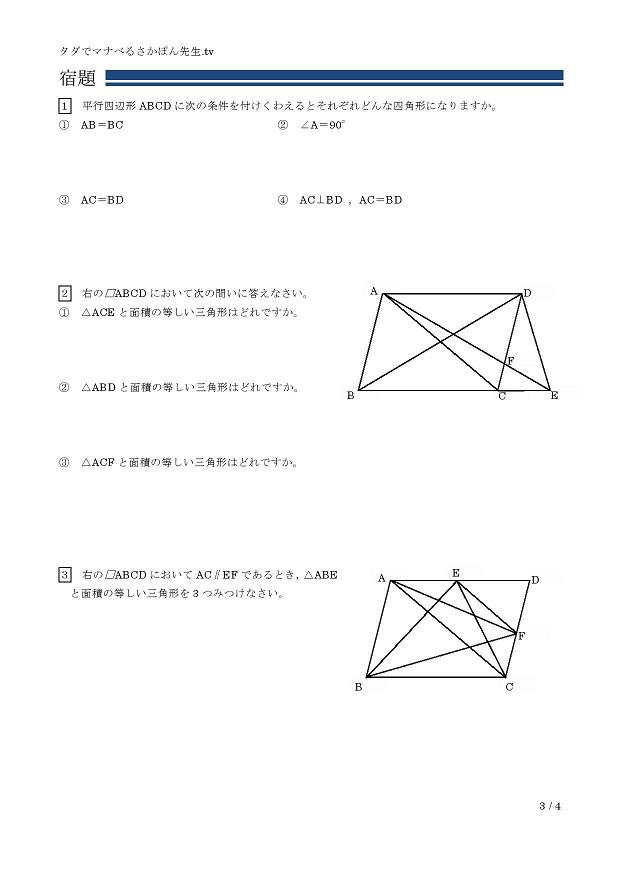



中学校2年生の数学の授業




平行四辺形 Wikipedia




図形の包摂関係 算数用語集




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



特別な平行四辺形2



2乗に比例する関数についてなんですけど 特別な四角形でない場合 正方形や Yahoo 知恵袋




特別な平行四辺形 四角の中の正pチュー 都立入試の情報満載 こじんまりしたこじま塾ブログ




中2数学 特別な平行四辺形145 147 中間期末テスト用 赤城 ᐡᐤᐡ




中2です 数学を教えてください 今 証明の中の特別な平行四辺形をや 中学校 教えて Goo




数学も英語も強くなる 意外な数学英語 Unexpected Math English Rhomboid




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



5 8e といてみよう 特別な平行四辺形 ホンわか先生



特別な平行四辺形1
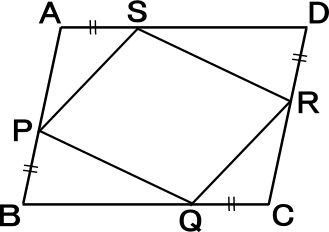



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同




中学2年生 特別な平行四辺形 公式 個別進学教室マナラボ受験 教育情報サイト



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形




特別な平行四辺形 四角の中の正pチュー 都立入試の情報満載 こじんまりしたこじま塾ブログ



Cms Oklab Ed Jp
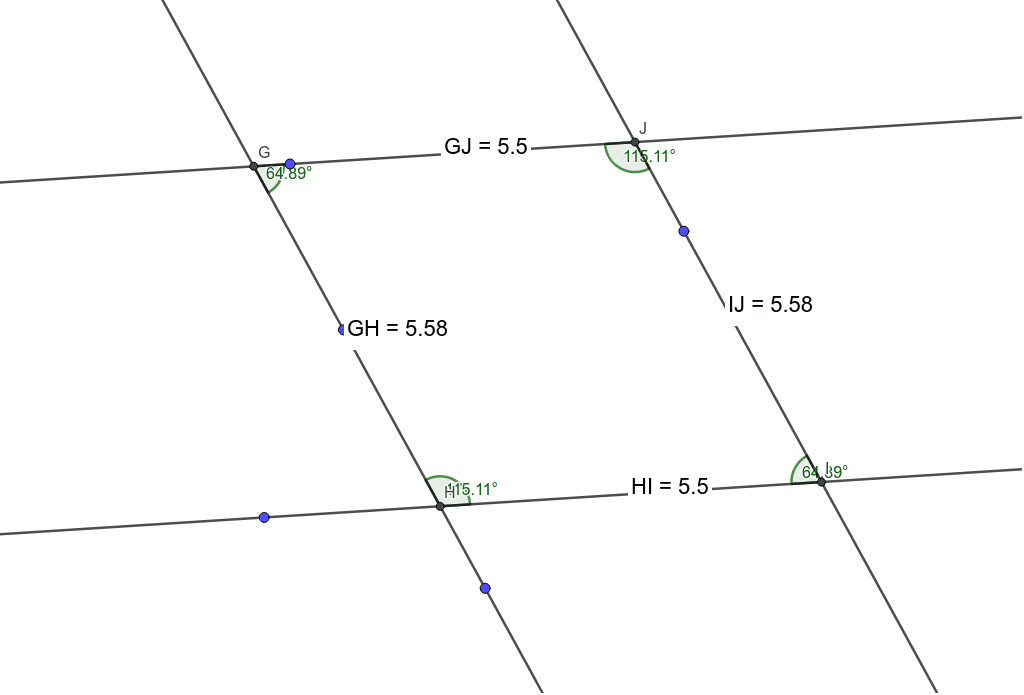



特別な平行四辺形 Geogebra




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




数学教材教具 特別な平行四辺形 対角線が変化すれば Youtube



Tsumugi Ne Jp
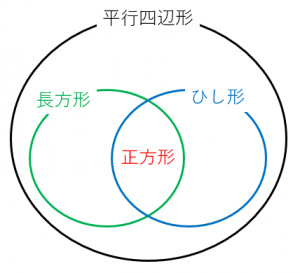



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学
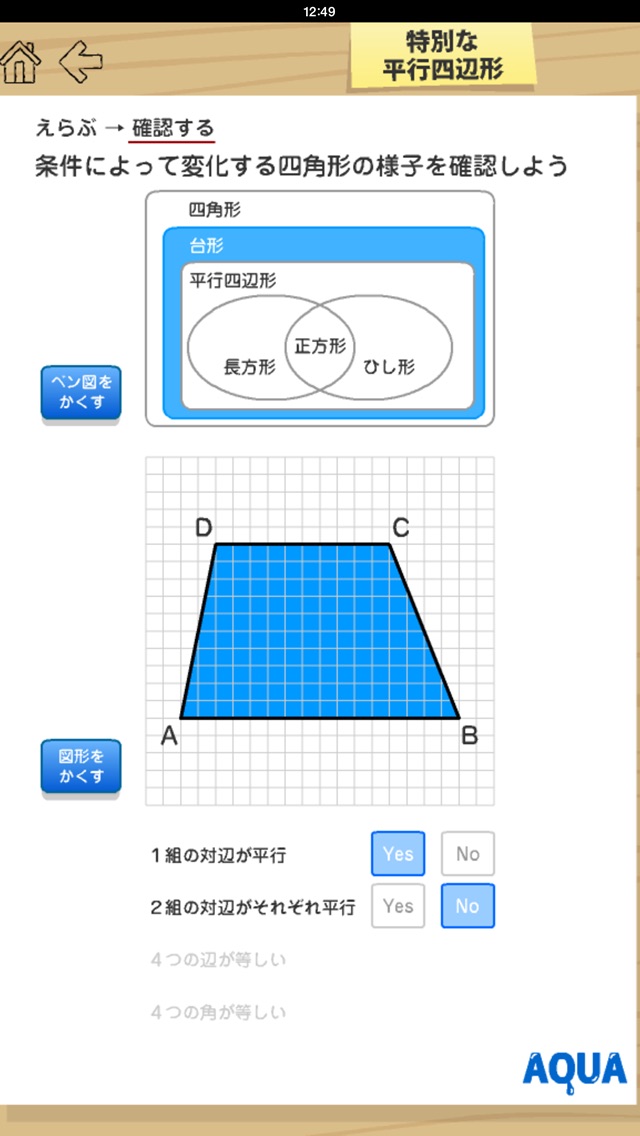



特別な平行四辺形 さわってうごく数学 Aquaアクア Iphoneアプリ Applion



Nyushi Sugaku Com



特別な平行四辺形この問題が分かる方は 必ず回答をお願いします 問 Yahoo 知恵袋



いろいろな四角形 四角形の対角線 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット
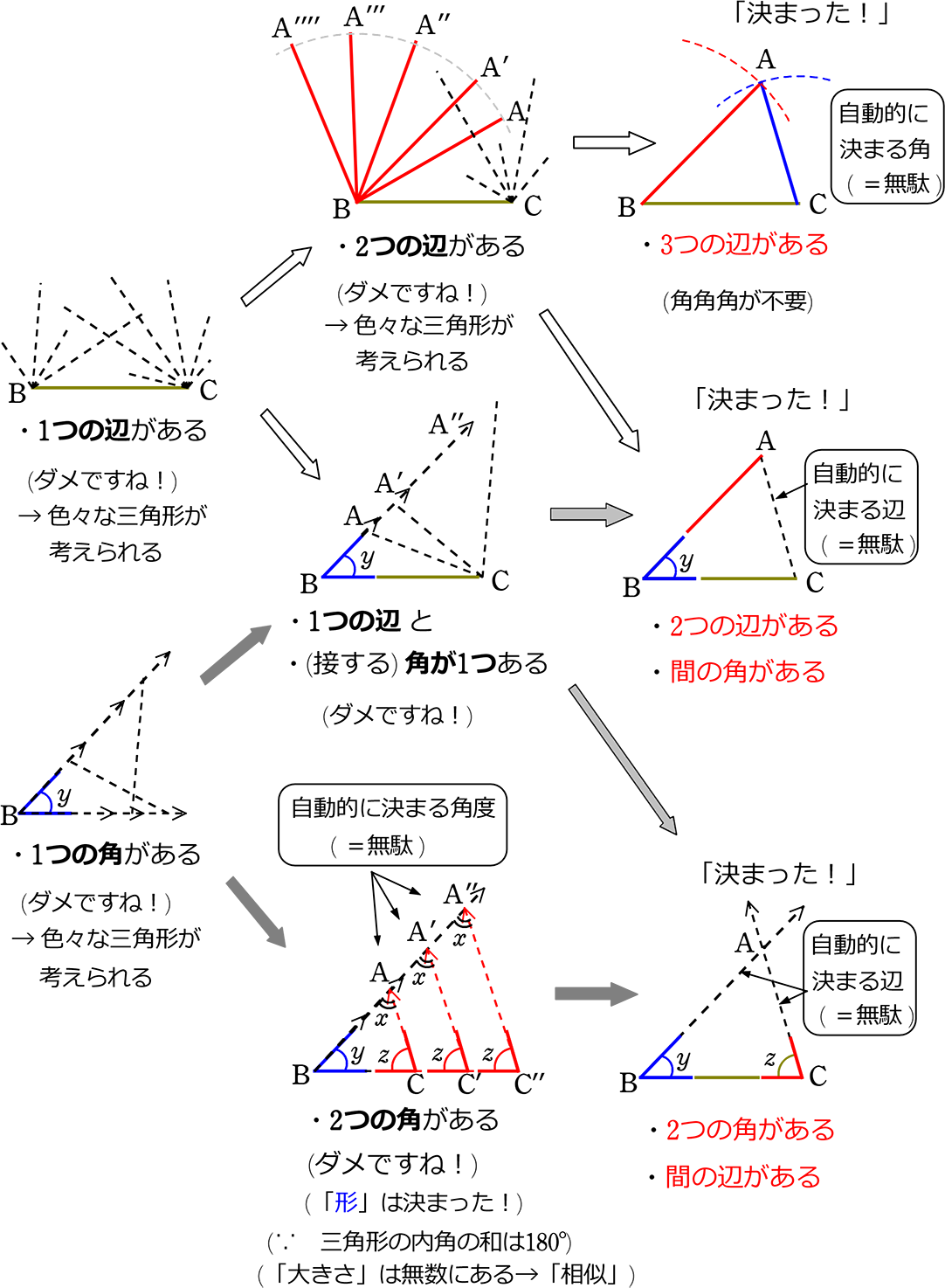



中学数学 図形の合同 図形の性質
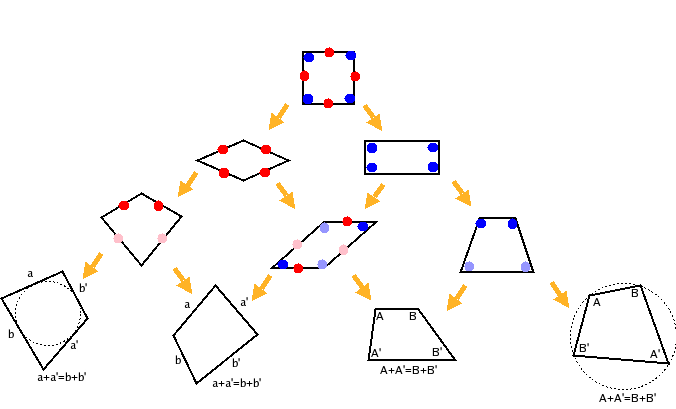



四角形の分類 低次元日記




平行四辺形の仲間を知ろう 電験3種web
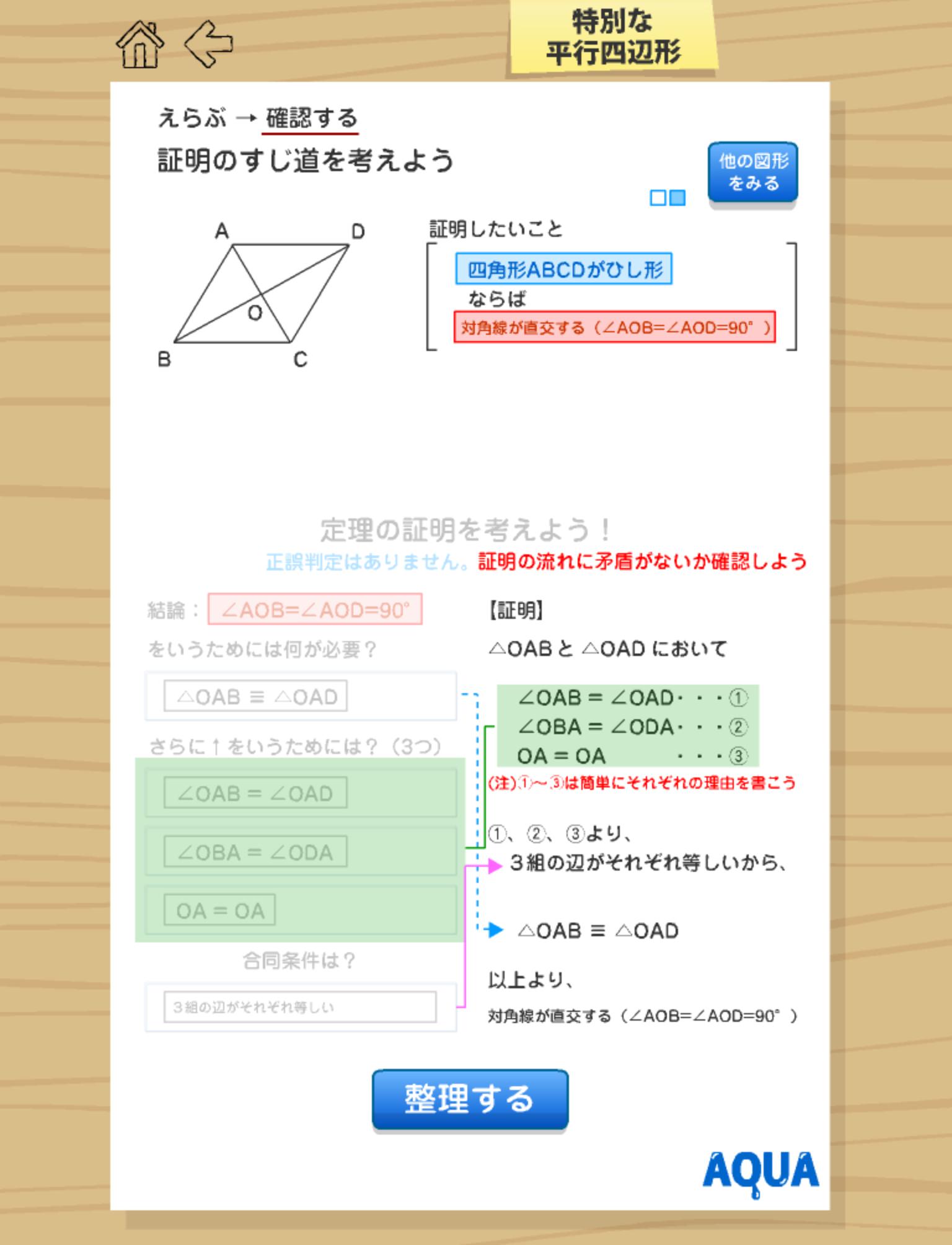



特別な平行四辺形 さわってうごく数学 Aquaアクア For Android Apk Download



特別な平行四辺形2
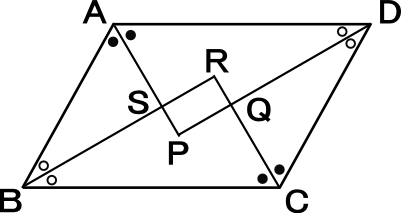



中学2年数学練習問題 平行四辺形 長方形 ひし形 正方形 の性質



Tsumugi Ne Jp
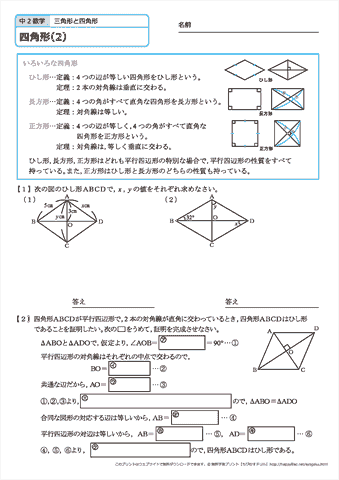



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中2の数学の問題で わからないところを教えてください 出題範囲三角形と四角 Yahoo 知恵袋
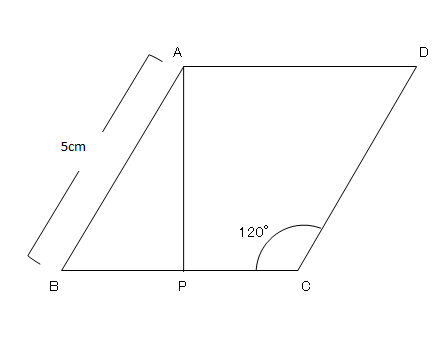



三平方の定理 特別な直角三角形 3 ネット塾




特別な平行四辺形 ドリるーむ




平行四辺形の定義と性質 証明問題の解き方 数学fun
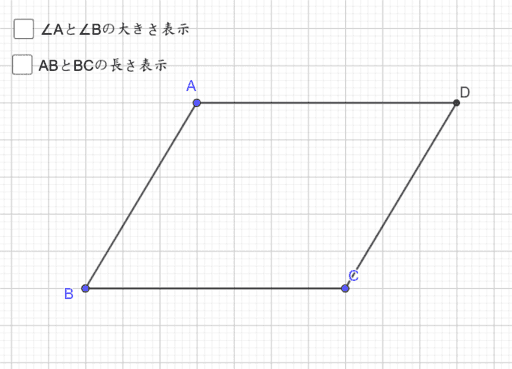



中2 平行四辺形 特別な平行四辺形 Geogebra




中2 特別な平行四辺形 平行線と面積 中学生 数学のノート Clearnote
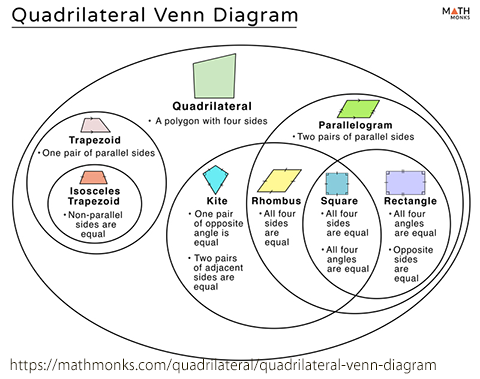



تويتر Kistenkasten723 على تويتر また 台形 Trapezoid のなかに 等脚台形を含めていることもある 陰山氏の分類には カイトはないが 氏は台形を平行四辺形 から独立させ 等脚台形に言及しているので これに近い 画像のように 正方形とひし形を凧形の特別な



平行四辺形の性質を使った証明 平行四辺形になることの証明 チーム エン



特別な平行四辺形 久保塾 今治市の学習塾 小学生 中学生 高校生 大学受験




中2 解きフェス 特別な平行四辺形 中学生 数学のノート Clearnote
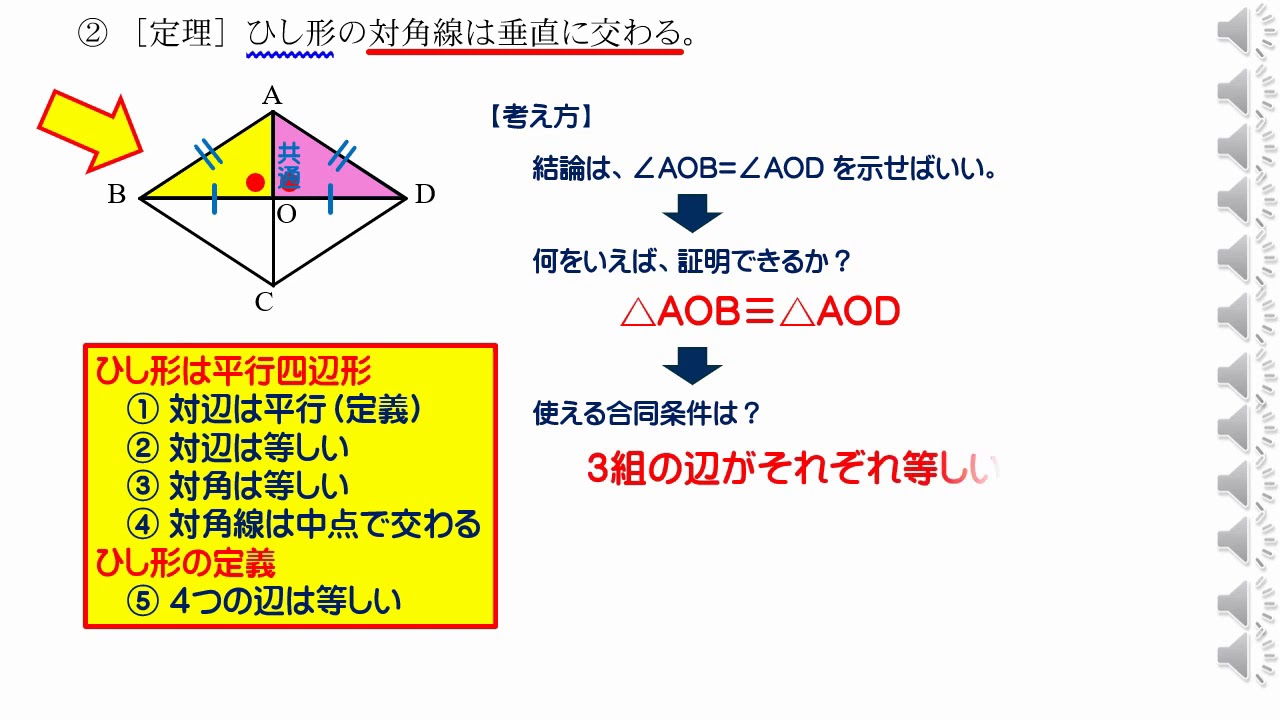



特別な平行四辺形 Youtube




特別な平行四辺形 さわってうごく数学 Aquaアクア For Android Apk Download




中学2年生数学 特別な平行四辺形 についてのまとめ 我流舎ウェブかわら版 川西市山下 個別指導塾 我流舎のブログ
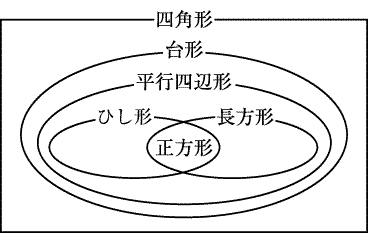



図形の包摂関係 算数用語集




この問題の意味詳しく教えてください エになるのは 分かるんですけど Clearnote




2 の解説をお願いします 答えは長方形です Clearnote



黒木玄 Gen Kuroki 掛算 そうそう 世の中には 教科書に書いてある通りの式だけが正しい公式である と思っている人もいるようですが 正しい公式かどうかを判定するための基準は 教科書に書いてあるかどうか ではなく 正しいか否か です 誤解して




中学 数学要点プリント冊子 メルカリ




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形




台形と平行四辺形を平行な辺の組の数で分類することは 原理的に不可能である 小学校4年生の算数 身勝手な主張
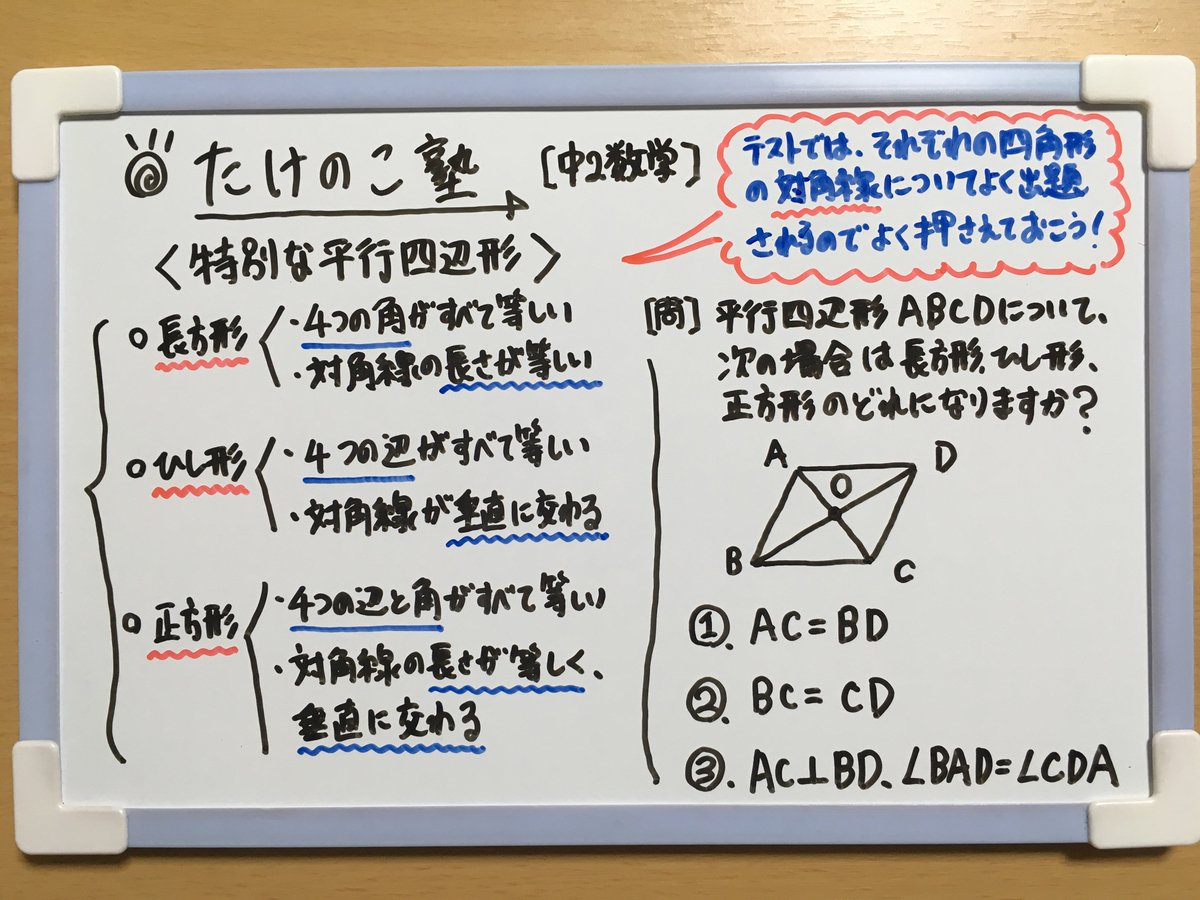



たけのこ塾 No Twitter 今回は 特別な平行四辺形 の問題です 長方形 4つの角がすべて等しく 対角線の長さが等しい ひし形 4つの辺がすべて等しく 対角線が垂直に交わる 正方形 4つの辺と角がすべて等しく 対角線の長さが等しく垂直に交わる 詳しくは画像に



5 8 特別な平行四辺形 ホンわか先生



1




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント



5章 三角形と四角形 タカラゼミ



3
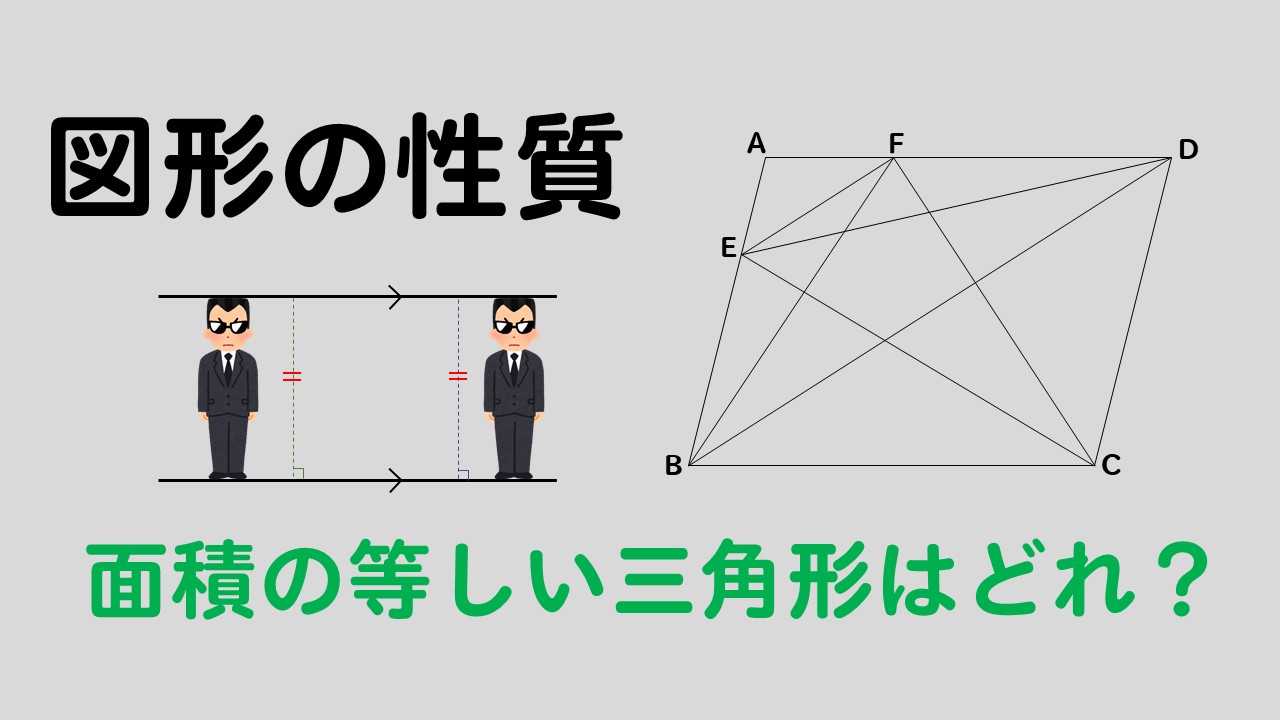



中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ
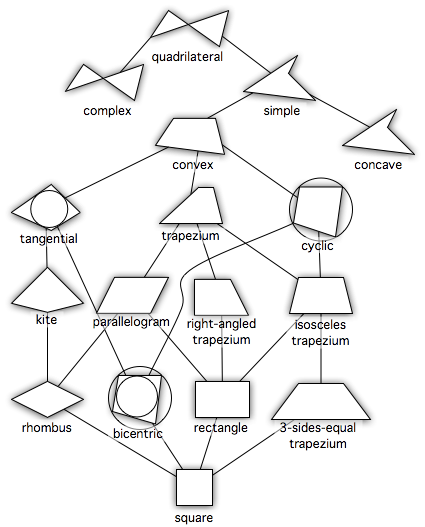



四角形 Wikipedia
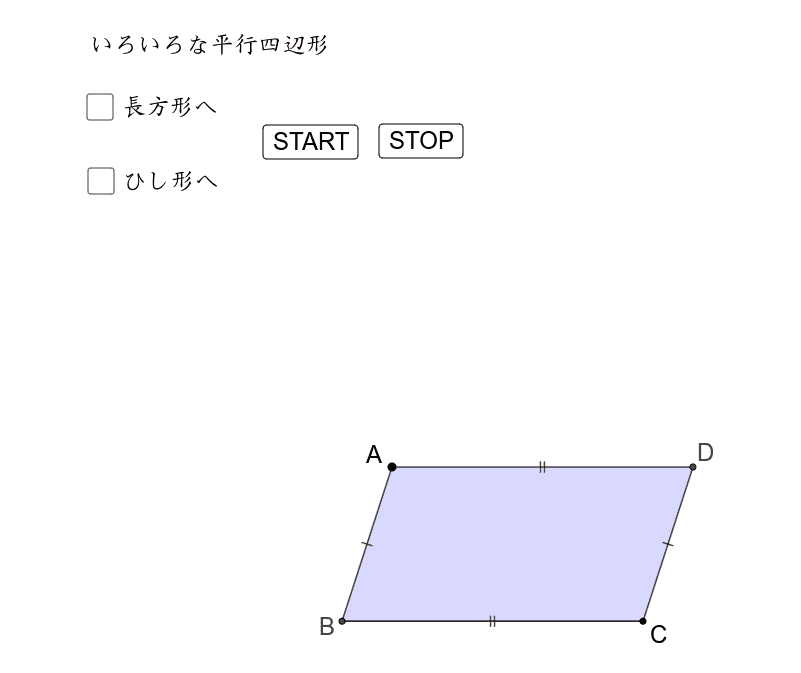



特別な平行四辺形への遷移 Geogebra




スプリックス 特別な平行四辺形 長方形 ひし形 正方形 4 Youtube




ボード 勉強 のピン




たけのこ塾 No Twitter 今回は 特別な平行四辺形 の問題です 長方形 4つの角がすべて等しく 対角線の長さが等しい ひし形 4つの辺がすべて等しく 対角線が垂直に交わる 正方形 4つの辺と角がすべて等しく 対角線の長さが等しく垂直に交わる 詳しくは画像に



特別な平行四辺形 チーム エン



0 件のコメント:
コメントを投稿