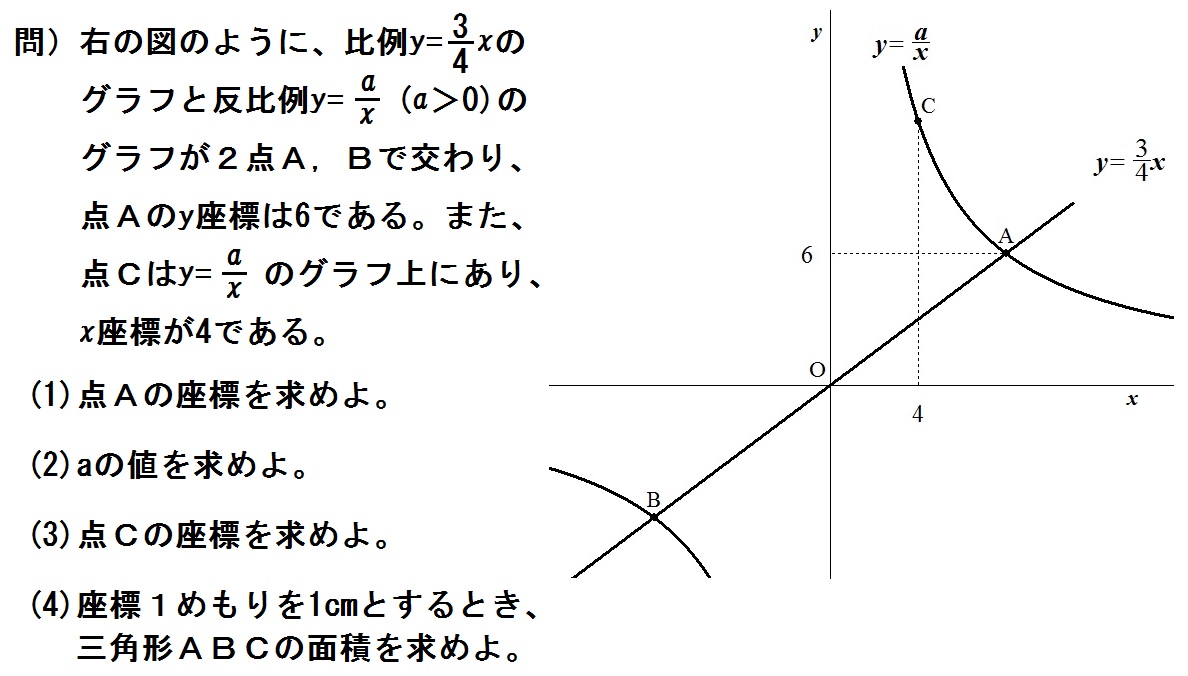
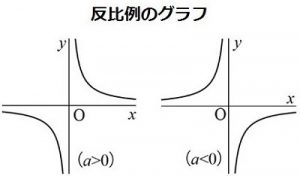
こんにちは、ウチダショウマです。 今日は、小学6年生および中学1年生で習う 「比例・反比例」 の式のグラフの書き方や比例定数の求め方、またそれらの意味や代表例についてわかりやすく解説していきます。 ※この記事では比例と反比例をセットで解説していきます。反比例の式の求め方 yがxに反比例し、xの値が4のときにyの値が2です。 このとき、yをxで表しなさい 反比例の式を求める問題 ですね。 比例の式 と同様、ステップをふんで考えてみましょう。 yがxに反比例することから、求める式を次のようにおきます。 (※aは定数です。 ) x=4のときにy=2なので、これをステップ1で作った式に代入します。グラフが双曲線だからxとyは反比例の関係。式はy=a/x とおけるね。 このグラフが通っている点を調べると、(2,5)を通っているね。 これを x、yに代入すれば、比例定数aが求められる んだよ。 aの値がわかったら、y=a/xの式に代入しよう。
無料 中1数学 テスト対策問題 問題プリント 123 比例と反比例4 反比例2グラフ
反比例 グラフ 式の求め方
反比例 グラフ 式の求め方-比例のグラフは原点を通る直線になりますが,原点を通る直線がかかれているとき,そのグラフは比例のグラフになります。 yがxに比例するとき,y=axのようにしてxとyの間の関係を式で表すことができます。そして,この式からさらに, a=y/x のように変形普通の目盛と対数目盛 普通のグラフでは, 二点間の距離がその二点の数値の差に比例するような目盛 (普通の数直線)を使います。 「1から0」「0から1」「1から2」はすべて同じ長さになります。 一方, 二点間の距離がその二点の数値の対数の差に比例するような目盛 を対数目盛と言います。



中学数学 比例と反比例 の教え方 比例の式を求める
中1数学。「反比例のグラフ」をかけ。「y = 6/x」ハァァ? x 軸にも y 軸にもくっつかない理解不能(ガクッ)おや、中学生が倒れそう。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 反比例など一発! コツを語る無料サイト。比例のグラフから式を求める方法 反比例の公式まとめ! 反比例のグラフの書き方、基礎からていねいにやってみよう! 反比例の式を作る簡単な方法を解説! 反比例の変域問題の解き方は?? 反比例の変化の割合って一定?求め方と考え方を解説!←今回・ 反比例 について 、式や表、グラフ からその 特徴 を考えることができる 。 ・ 反比例 の関係 を、 、 。具体例 を式に表すことを 通して 一般化 し説明 することができる ()3 数学的 な表現 ・処理 ・ 反比例 の関係 を式で表すことができる 。
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru反比例の式とグラフの書き方 反比例の式から、グラフを書きましょう。比例や反比例の式をグラフにするのは、案外簡単です。反比例の式にxの値を入れて、その値から求まるyの値をプロットし、線をつなぐだけです。 例えば、 y=1/x という式があります。比例のグラフから式を求める方法 反比例の公式まとめ! 反比例のグラフの書き方、基礎からていねいにやってみよう!←今回の記事 反比例の式を作る簡単な方法を解説! 反比例の変域問題の解き方は?? 反比例の変化の割合って一定?求め方と考え方を
エクセルで反比例のグラフを描く方法 求められた計算結果をもとに、反比例のグラフを作成していきましょう。 xとy両方の数値範囲を選択し、上タブの挿入、散布図、平滑線と選んでいきます。 すると、以下のような反比例のグラフができました。 後は反比例も直角双曲線 中学数学で習う反比例のグラフ y = k x y=\dfrac{k}{x} y = x k も直角双曲線です。 x 2 − y 2 = a x^2y^2=a x 2 − y 2 = a というタイプの直角双曲線を 4 5 ∘ 45^{\circ} 4 5 ∘ 回転させると反比例のグラフになるからです(後できちんと証明します)。反比例のグラフから、式を求めよう 「『yはxに反比例』を式で表す問題」 を学習しよう。 これまで反比例の問題では、式をグラフで表したり、グラフを式で表したり、といったことをやってきたね。



反比例とは グラフの描き方や式の求め方をわかりやすく解説します Studyplus スタディプラス




反比例のグラフ 読み取り 式の作り方と書き方を解説 中学生 中学数学 理科の学習まとめサイト
あとは、反比例の式である y=a/x の x の上に乗っけてやればよって、反比例の式は $$\color{red}{y=\frac{8}{x}}$$ となります。 また、\(xy=a\) となることを覚えておけば $$a=2\times 4=8$$ よって、反比例の式は $$y=\frac{8}{x}$$ このように求めることができます。 グラフから座標を読み取る。16時 反比例の式表示 17時 反比例のグラフのかき方と考察 18時 比例と反比例の関係をまとめる 19・時 練習、たしかめ道場 小6年 比例と反比例 実験をとおした変化の実感と中学校への接続を大切にした指導 関連する単元



比例 反比例 デジタル教科書 電子教科書




中1数学 反比例のグラフ 練習編 映像授業のtry It トライイット
数学14章比例・反比例「反比例の表,式,グラフ」<準備問題> 組 番 名前 1次の(1)~(3)について,yをχの式で表しなさい。また,このうちyがχに反 比例するものを選びなさい。 (1)面積が12㎝2の長方形の縦の長さをχ㎝,横の長さy㎝。 グラフが通る点を取っていくために、まずは反比例の式に\(x=1\)を代入します。 \(x=1\)を \(\displaystyle{y=\frac{6}{x}}\)に代入すると $$y=\frac{6}{1}=6$$ このことから、反比例のグラフは\(x=1\)のとき\(y=6\)を通るということが分かります。問題 比例について 式を求めましょう。 グラフを書きましょう。 グラフを利用して座標を求めましょう。




反比例のグラフから式を求める チーム エン




中1 数学 中1 53 反比例のグラフを書く 読みとる Youtube
反比例の式を求める yがxに反比例するとわかっている場合、対応するxとyの積で比例定数を求める。 xy = a 例 yがxに反比例し、x=4のとき、y=6である。反比例の式を求めよ。 xy = 4×(6)=24より y = 24 x 確認次の問いに答えよ。 答表示 yがxに反比例し、x 比例反比例のグラフの練習問題です。反比例のグラフの書き方のポイント・反比例のグラフは比例定数の公約数の組み合わせ求めて点を打っていくと書きやすくなります。例)比例定数が6のとき (1、6) (2、3)(1、6) (2、3)に点を打つ。「双曲線の式を求める問題」 を学習しよう。 y=a/xという反比例の式から、双曲線のグラフをかく方法は、1つ前の授業で学んだよね。 今回はその逆。双曲線のグラフから式を求めるパターンなんだ。



いざ いざ 実践 比例と反比例 小学6年 算数の教え方教えますmother S Math Happy Study Support




比例 と 反比例 の 利用 中学生必見 数学の無料プリント 復習用に 比例と反比例 Amp Petmd Com
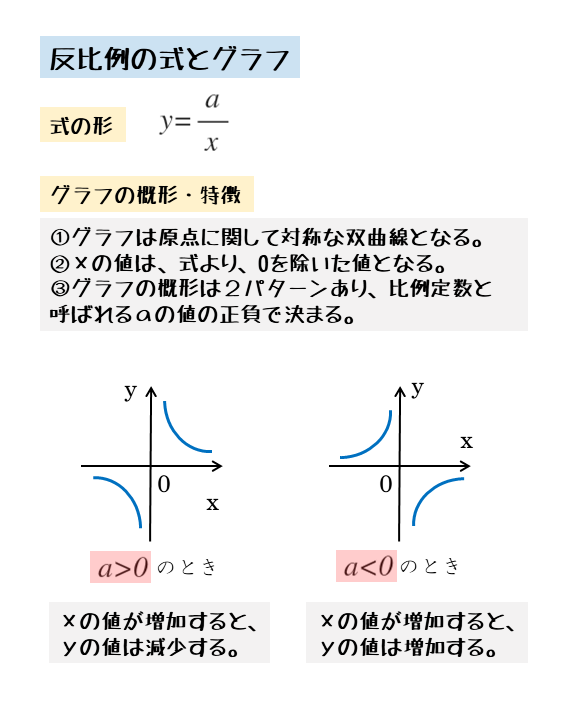
グラフで表現すると、曲線の形になる → 双曲線 \(x\)や\(y\)が0になることはない;や,グラフから比例の 式を求めることができ るようにする。 1組のx,yの値 から比例の式を求め る。 比例を表すグラフ から,比例の式を求 める。 技1組のx,yの値 や,グラフから比例の式を 求めることができる。 9 基本の問題 10 3 反比例中1数学。「y は x に反比例し」「y を x の式で」ハァァ?? 分からん(ガクッ)おや、中学生が倒れそう。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 「反比例の式」の2つの形、比例定数 a も一発! コツを語る無料サイト。



反比例とは 式やグラフの書き方 記号 問題の解き方 受験辞典



反比例の表とグラフ 教遊者
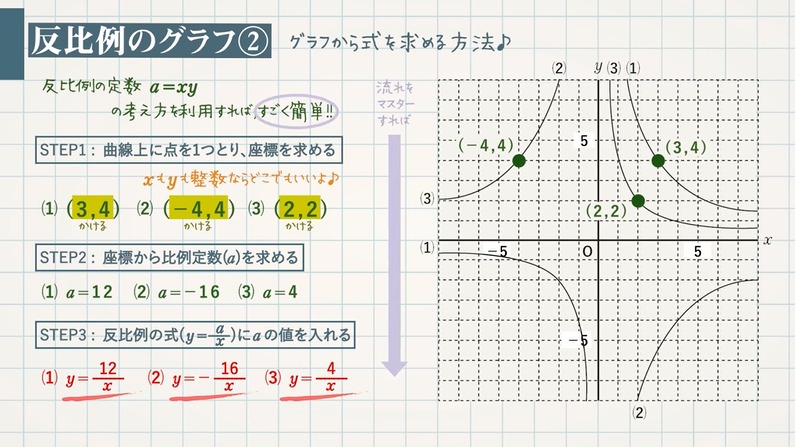
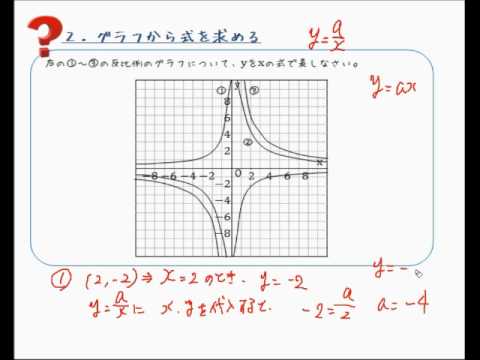
反比例の式"a=xy"を押さえよう! 実は、 "a = xy" という形の 反比例の式を使えば、 簡単に求められるんです。 「えっ?反比例の式って " y=a/x (x 分の a)"ではないの?」 と思った中学生もいるでしょう。 でもそんな皆さんは、 比例のグラフから式を求める方法←今回の記事 反比例の公式まとめ! 反比例のグラフの書き方、基礎からていねいにやってみよう! 反比例の式を作る簡単な方法を解説! 反比例の変域問題の解き方は?? 反比例の変化の割合って一定?求め方と考え方を解説!X y O ① ② 2 2 3 3 ① グラフ上にx=1の点をとる。 座標は (1, 2)である。 これは原点からx方向に+1進んだら y方向に2進むことになる。 このとき比例定数a=2となる。 つまりy=2x ② グラフ上にx=1の点をとる。 座標は (1,3)である。 これは原点からx方向に+1進んだら




中1数学 双曲線の式の求め方 例題編 映像授業のtry It トライイット




中1数学 比例のグラフ1 Y 2xなど 映像授業のtry It トライイット
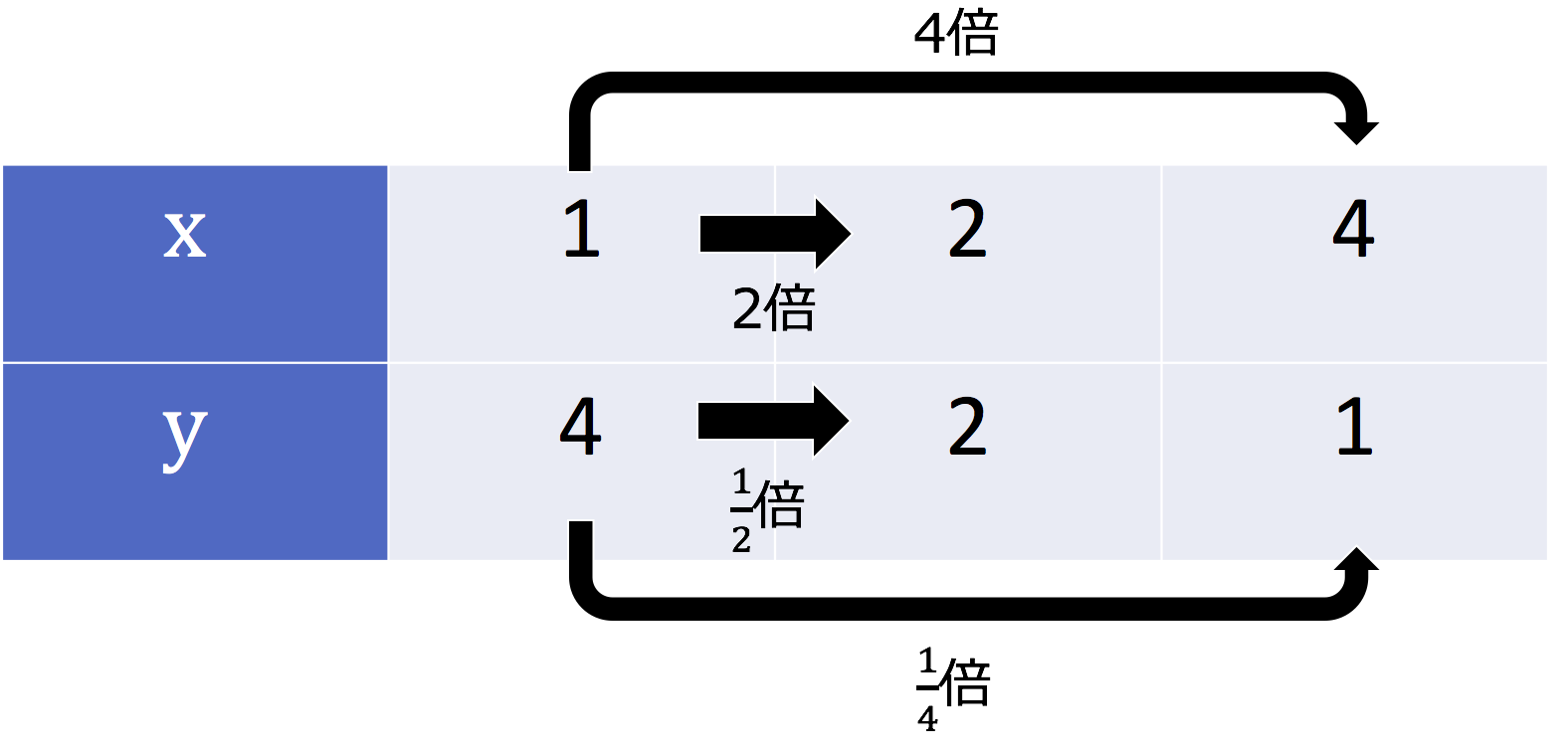
反比例の公式 \(y=\frac{a}{x}\) (ただし、比例定数は\(a\)) 反比例の性質 一方の変数が2,3倍になると、もう一方の変数は1/2,1/3倍になる;が に反比例するとき、 と の関係は、 =きまった数÷ という式で表します。 教え方3 の式を使って、反比例の関係をグラフで表す方法を教えます。 そして反比例のグラフは比例のグラフのように直線にならないことに気づかせます。 ※グラフのめもりのグラフが分かっている時の式の求め方 例1この反比例のグラフの式を求めなさい。 比例のグラフが示されていて、比例定数が分からない時、どのように式を導出すればよいでしょうか。 これは意外と簡単です。 反比例の式は $$y=\frac{a}{x}$$ と表されます。



3



反比例とは グラフの描き方や式の求め方をわかりやすく解説します Studyplus スタディプラス
次の式に対応するグラフをクリックしてください. 解説 やり直す の式で表されるグラフは,双曲線と呼ばれ,1組の(2つの)グラフになります.したがって,直線のグラフは答になりません. 反比例のグラフから式を求めるのは、そう難しいことではない。 やっている作業だけ見れば、「一点座標を取って、 x x と y y をかけ算し、 a a を求めて式を作れば終わり」である。反比例のグラフ(1) 反比例のグラフ(2) 反比例のグラフの式 練習問題(1) 練習問題(2) 比例と反比例の活用(1) 比例と反比例の活用(2)



中1数学 反比例の式 グラフってどういうもの まなビタミン
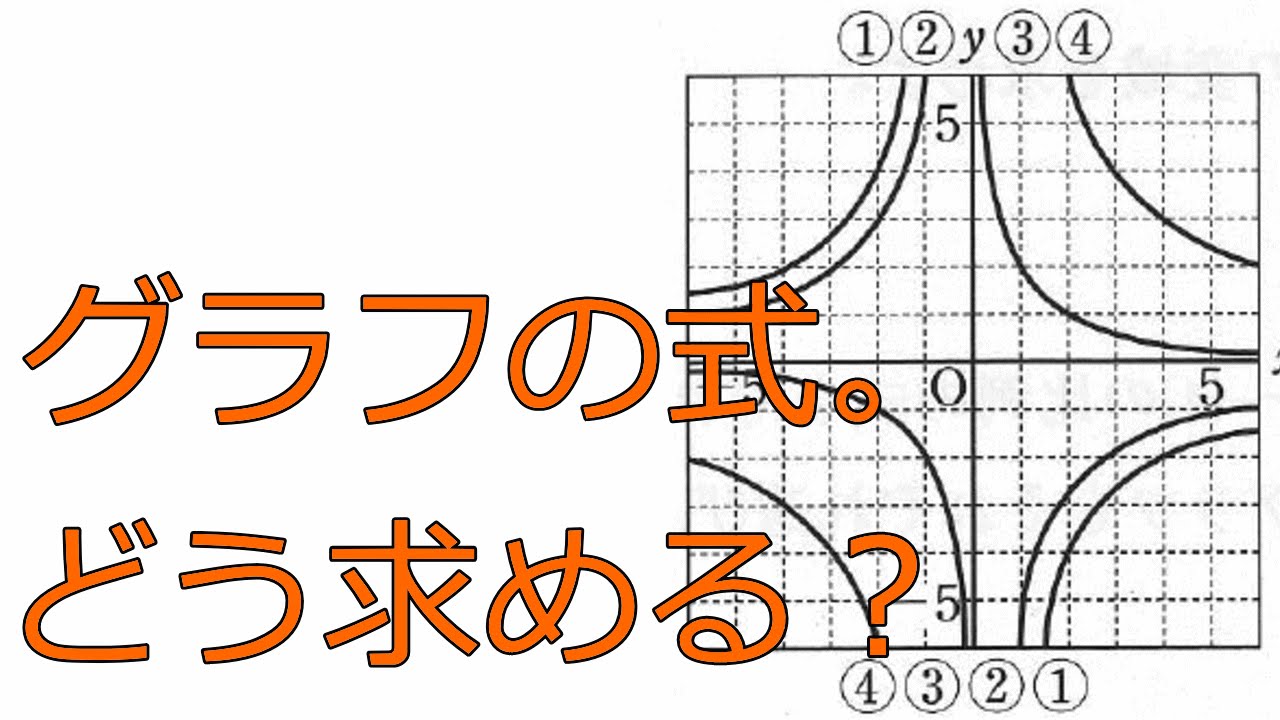



反比例のグラフと式の求め方 中学1年数学 Youtube



数学のねっこ 4 2 反比例とそのグラフ 練習問題
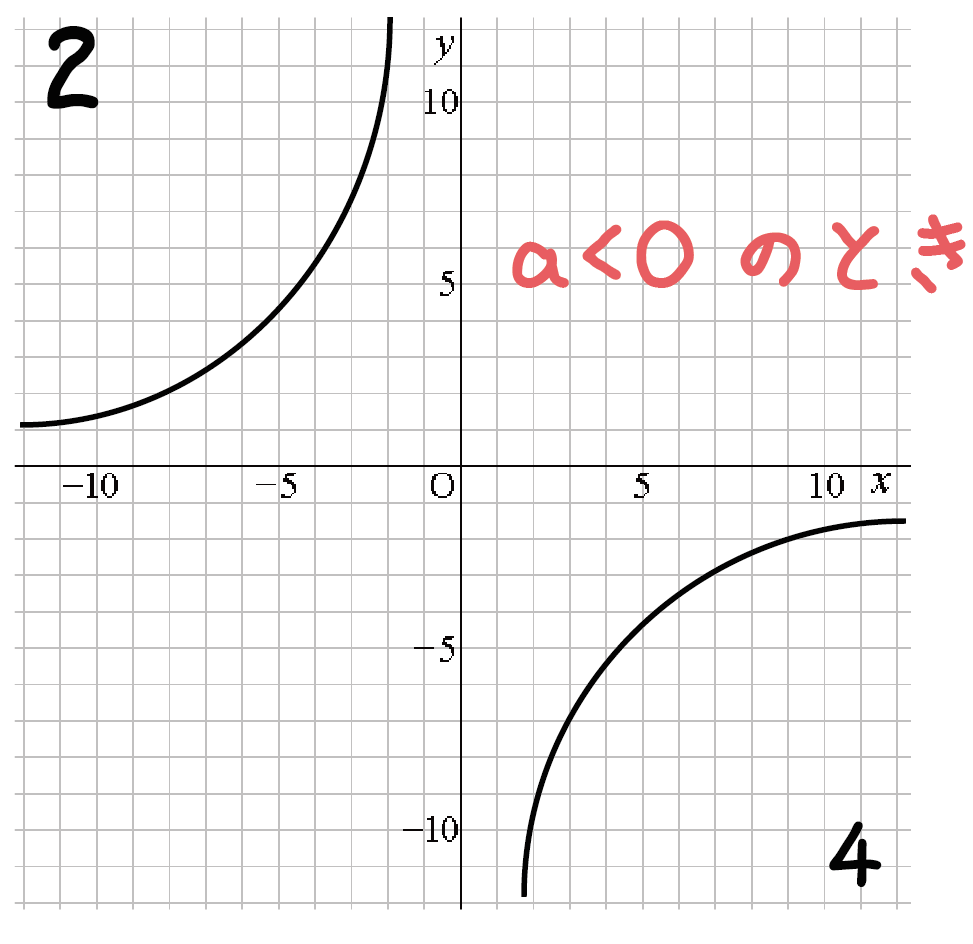



中1数学 反比例のグラフにみられる3つの特徴 Qikeru 学びを楽しくわかりやすく




反比例とは何かが例で即わかる 公式 グラフの書き方も即理解 高校生向け受験応援メディア 受験のミカタ



無料 中1数学 基本問題 解答プリント 比例と反比例5 反比例のグラフ 132
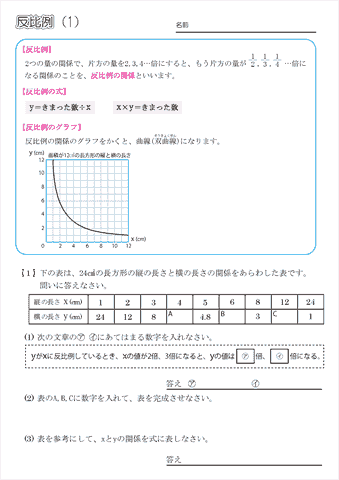



小学6年生の算数 反比例 練習問題プリント ちびむすドリル 小学生




中1 数学 中1 51 反比例の式 基本編 Youtube



Mathematics 比例と反比例 式と座標 働きアリ
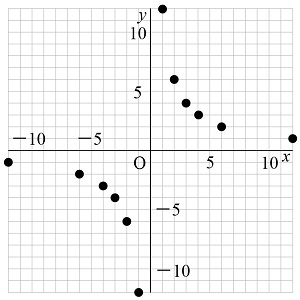



中1数学 反比例の式 グラフってどういうもの まなビタミン
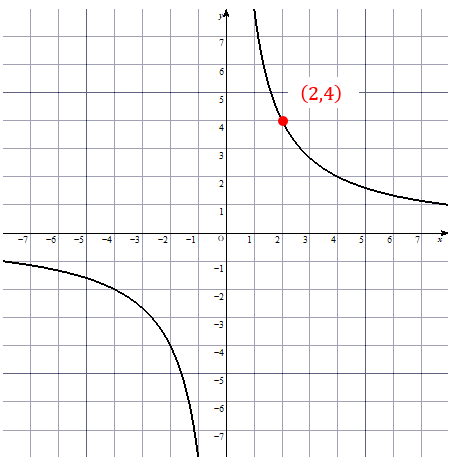



比例 反比例の式 式の作り方 違いは 問題を使って解説するぞ 数スタ




中学数学 比例 反比例



Studydoctor反比例のグラフと式の求め方 中学1年数学 Studydoctor
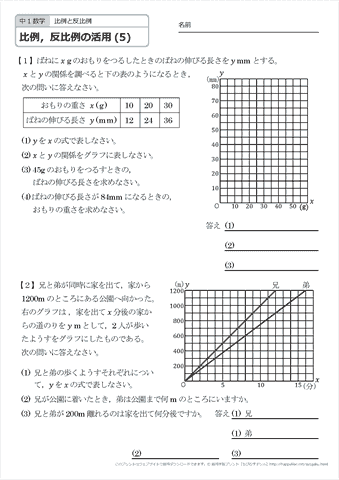



比例 と 反比例 の 利用 中学生必見 数学の無料プリント 復習用に 比例と反比例 Amp Petmd Com




3 2 8 Descubre Como Resolverlo En Qanda



反比例の式は 1分でわかる意味 特徴 解き方 グラフの書き方 分数との関係



比例 反比例の式を求める練習問題 ファクトリウム




比例と反比例 中学数学の座標の読み方とグラフの式の求め方 リョースケ大学



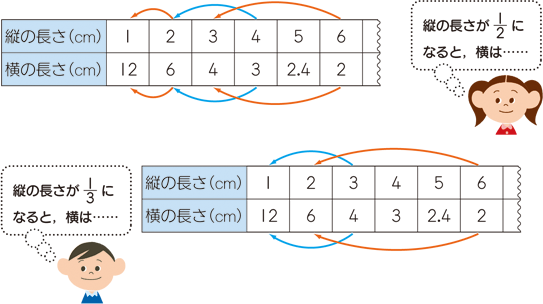
表 グラフから反比例の式を求める 考え方 デジタル教科書 電子教科書



無料 中1数学 テスト対策問題 問題プリント 123 比例と反比例4 反比例2グラフ




比例と反比例はこれで完璧 グラフと式の読み解き方




中1 中1が作った中1のレポート 比例 反比例 中学生 数学のノート Clear




比例と反比例 小6 式に慣れ グラフを知る 算数の教え方教えますmother S Math Happy Study Support
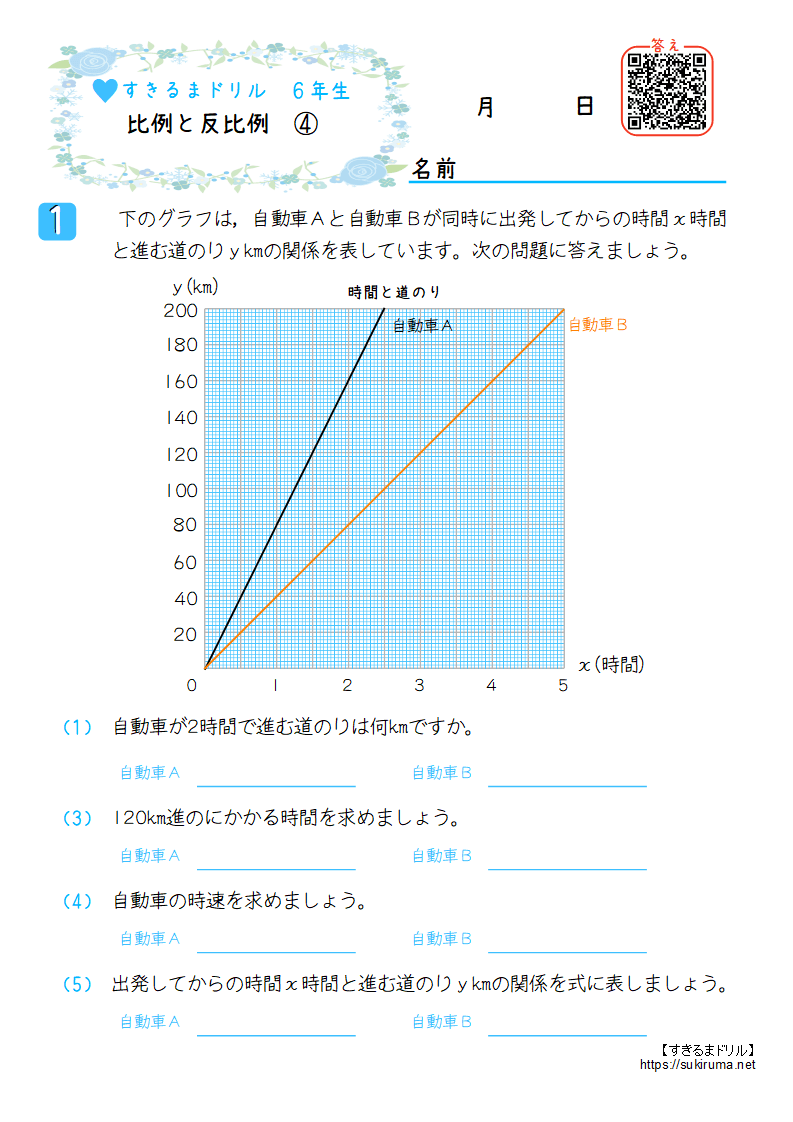



すきるまドリル 小学6年生 算数 比例と反比例 無料学習プリント すきるまドリル 無料学習プリント



中1数学 反比例の式 グラフってどういうもの まなビタミン



1




標準 反比例のグラフ なかけんの数学ノート



グラフから式を求める 反比例 Youtube




反比例の式のグラフとは 比例定数の求め方 意味や例について解説 遊ぶ数学




中1数学 反比例の式 グラフってどういうもの まなビタミン




比例と反比例 6 反比例のグラフ 伊東市の家庭教師




反比例のグラフからaを求める問題 あるいは変域を求める問題が分かりません Clear
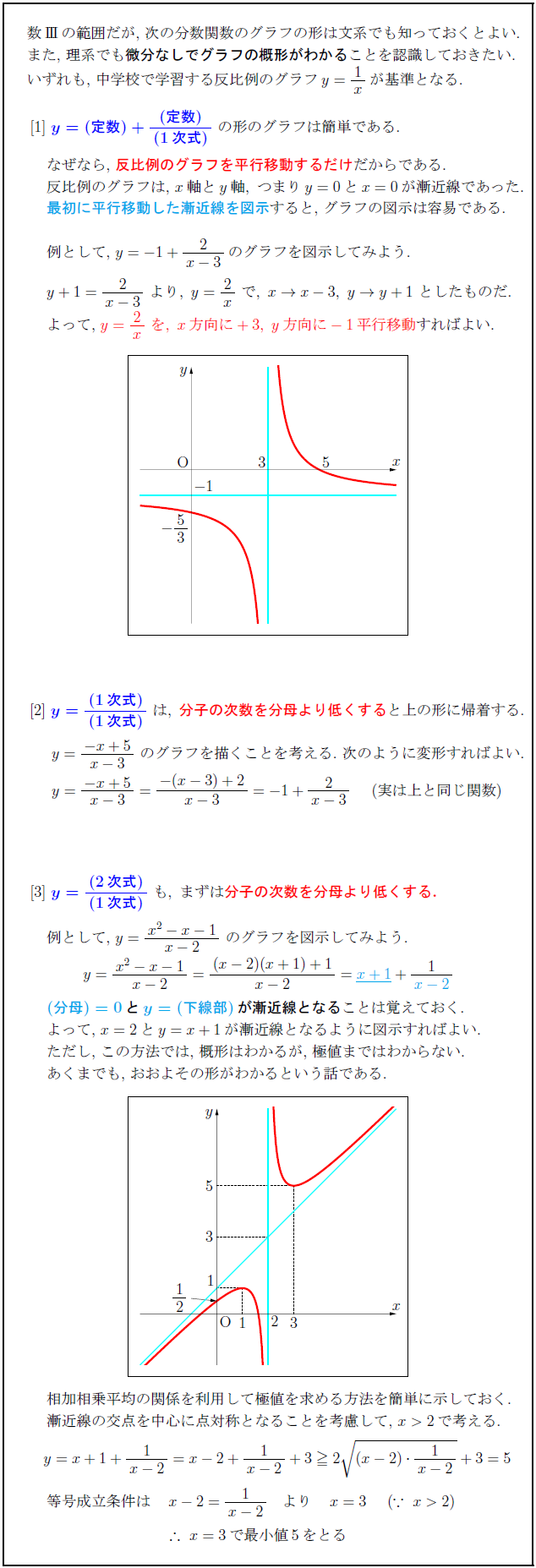



高校数学 文系も知っておくべき基本的な分数関数 数 のグラフ 受験の月




中1数学 反比例の式 グラフってどういうもの まなビタミン
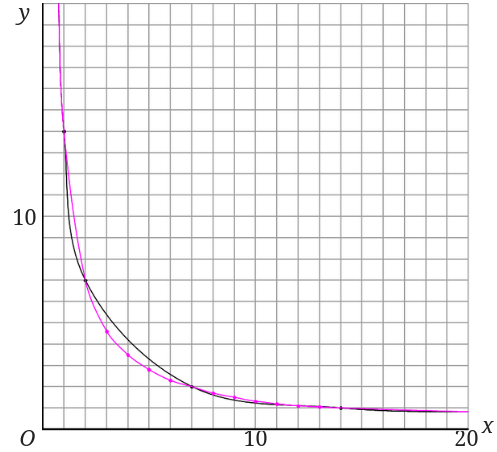



小学生に教える反比例のグラフの書き方と見落としがちな特徴 みけねこ小学校




2vx Y Lihat Cara Penyelesaian Di Qanda




反比例の式とグラフ 数学fun




比例と反比例1b 学習ノート 学習 数学ノート




小6 算数 小6 34 反比例のグラフ Youtube



無料 中1数学 基本解説 解答プリント 比例と反比例5 反比例のグラフ 132



反比例とは グラフの描き方や式の求め方をわかりやすく解説します Studyplus スタディプラス
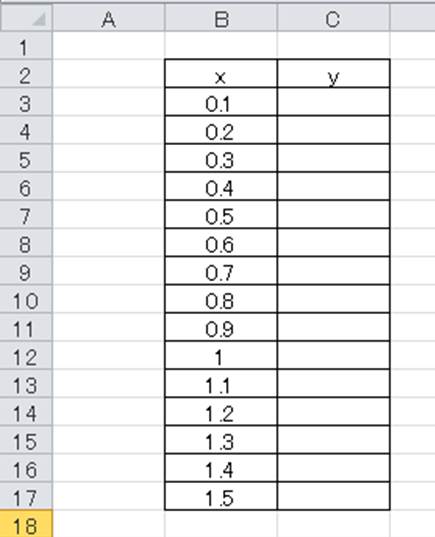



Excel エクセルで反比例のグラフや表を作成する方法



1




一次関数とは 式とグラフの解説 数学fun




3分で分かる 反比例とは 反比例のグラフの書き方 反比例の式など 合格サプリ



比例 反比例のグラフ作成 個人的健忘録 From 13



3分で分かる 反比例とは 反比例のグラフの書き方 反比例の式など 合格サプリ




比例と反比例の違いは 見分け方はどうすれば良いか解説 数スタ




中1数学 双曲線の式の求め方 練習編 映像授業のtry It トライイット
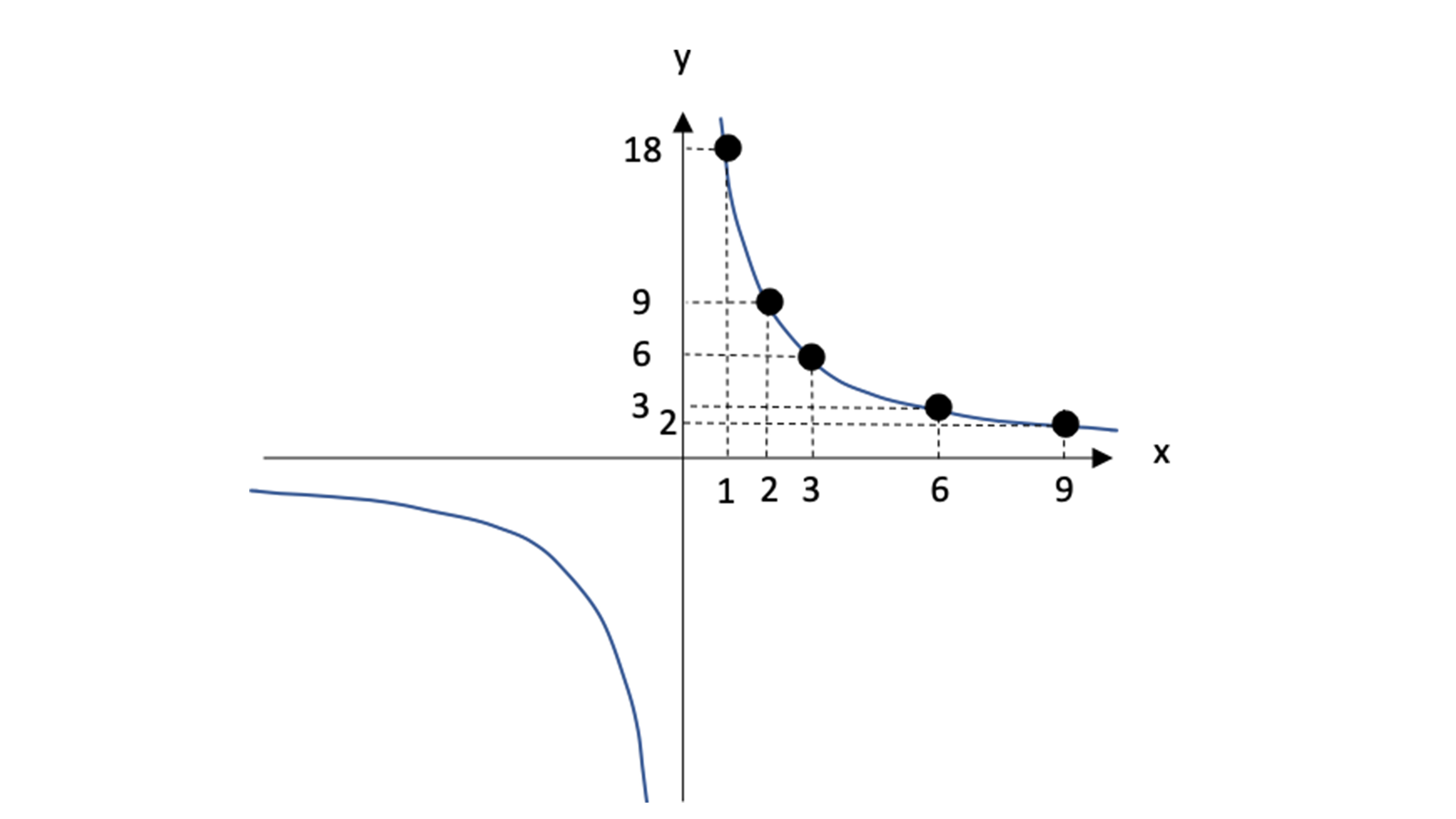



グラフが2本になるのに注意 比例 反比例 をおさらいしよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス
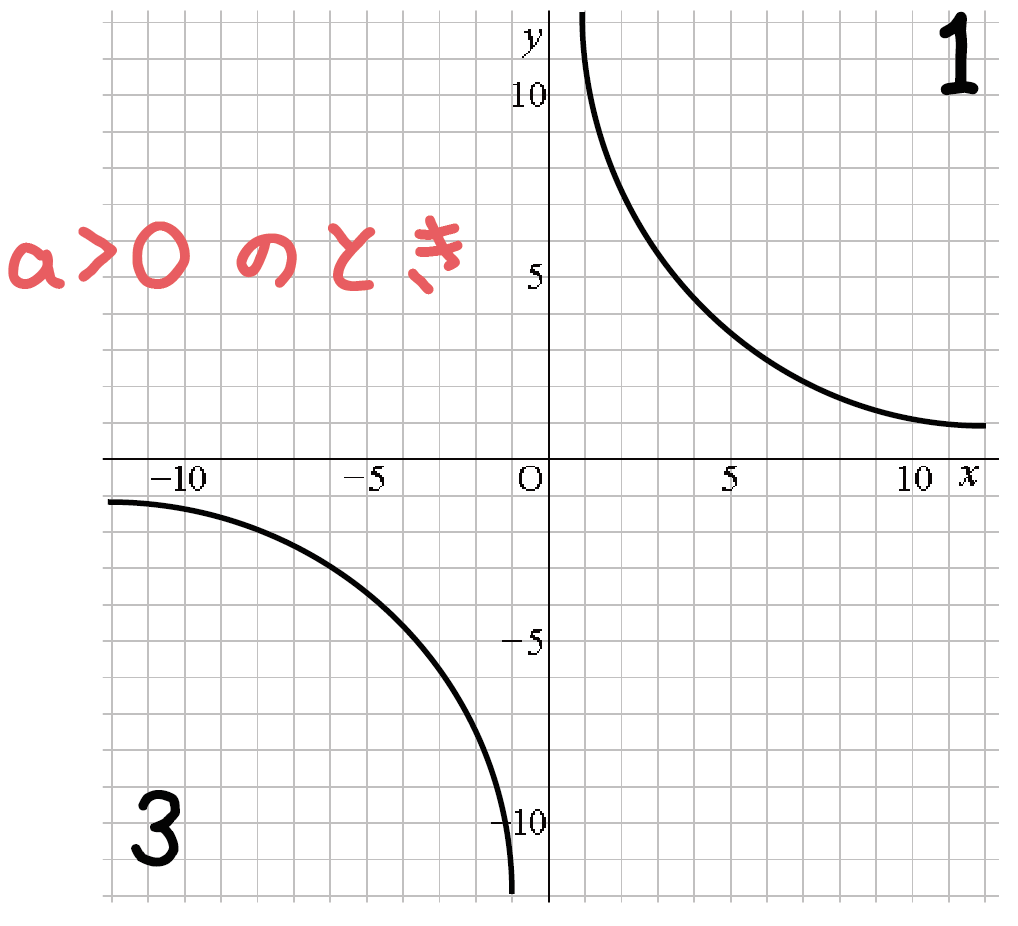



中1数学 反比例のグラフにみられる3つの特徴 Qikeru 学びを楽しくわかりやすく



Mathematics 比例と反比例 式と座標 働きアリ




3 2 8 Descubre Como Resolverlo En Qanda



無料 中1数学 基本問題 解答プリント 比例と反比例4 反比例の式 131




第8回 すなおな反比例 後編 数学ガールの秘密ノート 結城浩 Cakes ケイクス




中学校数学 1年生 数量 比例と反比例 Wikibooks



比例と反比例 まとめ4 中学から数学だいすき



2次関数 関数について 日々是鍛錬 ひびこれたんれん



反比例式とグラフ デジタル教科書 電子教科書




応用 比例と反比例のグラフ なかけんの数学ノート




Lm X 1 Y O Left 1right Descubre Como Resolverlo En Qanda



反比例 算数用語集



Search Q E4 B8 80 E6 Ac A1 E9 96 E6 95 B0 Tbm Isch



任意の2点の通る反比例のグラフの式を求めたいのですがどうした Yahoo 知恵袋
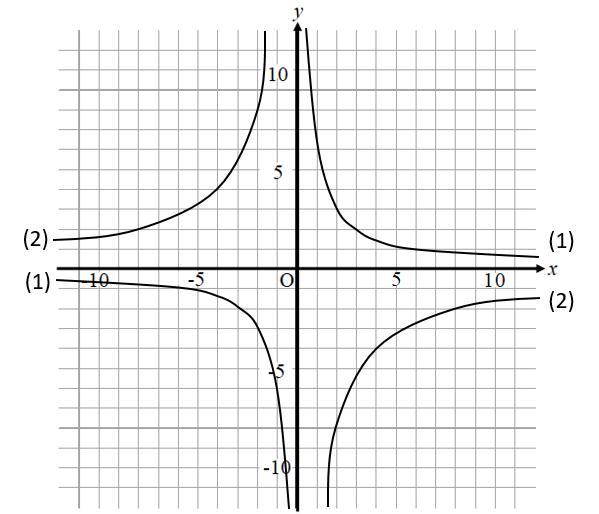



反比例 式を作る Aを求める 方法はたったコレだけ グラフからの読み取りも簡単 数スタ




中学校数学 1年生 数量 比例と反比例 Wikibooks




中学数学 比例と反比例 の教え方 比例の式を求める



Studydoctor比例 反比例のグラフと図形 中学1年数学 Studydoctor
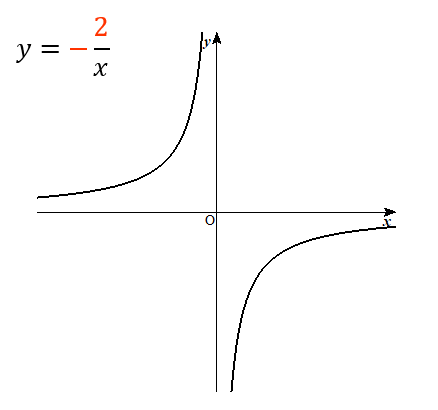



反比例のグラフの書き方 基礎からていねいにやってみよう 数スタ
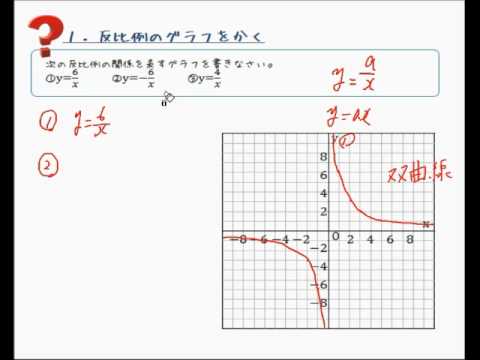



反比例のグラフをかく Youtube




反比例の形をしたグラフの求め方 数学の問題で 一般式は次のように 数学 教えて Goo




比例の式と反比例の式 Geogebra




書き方 反比例の双曲線グラフを5秒でかきおえる方法 Qikeru 学びを楽しくわかりやすく




反比例 By S W




中学校数学 1年生 数量 比例と反比例 Wikibooks




比例と反比例はこれで完璧 グラフと式の読み解き方



Studydoctor反比例のグラフと整数点の個数 中学1年数学 Studydoctor



無料 中1数学 標準問題 解答プリント 133 比例と反比例6 利用1
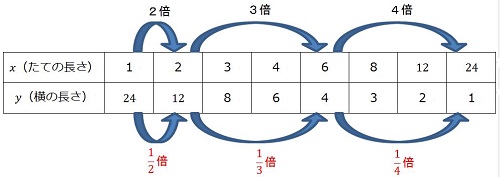



中1数学 反比例の式 グラフってどういうもの まなビタミン



反比例とは グラフの描き方や式の求め方をわかりやすく解説します Studyplus スタディプラス




書き方 反比例の双曲線グラフを5秒でかきおえる方法 Qikeru 学びを楽しくわかりやすく
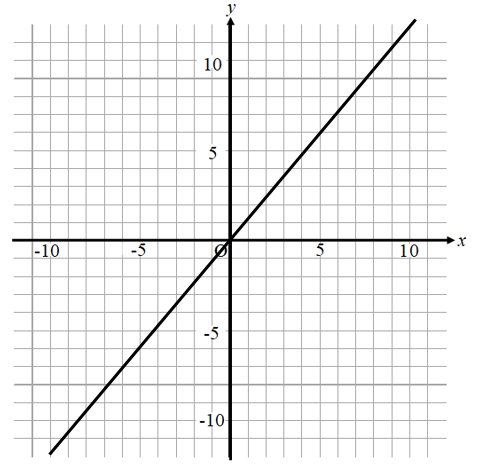



比例のグラフから式を求める方法とは ラクな裏技の考え方とは 数スタ
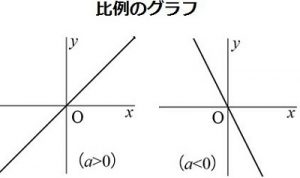



中1数学 反比例の式 グラフってどういうもの まなビタミン




比例 反比例 一次関数 二次関数 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信




写真のような比例 反比例のグラフで グラフに書きこみなさい や グラフの式を求め Clear



無料 中1数学 テスト対策問題 解答プリント 121 比例と反比例2 比例2グラフ
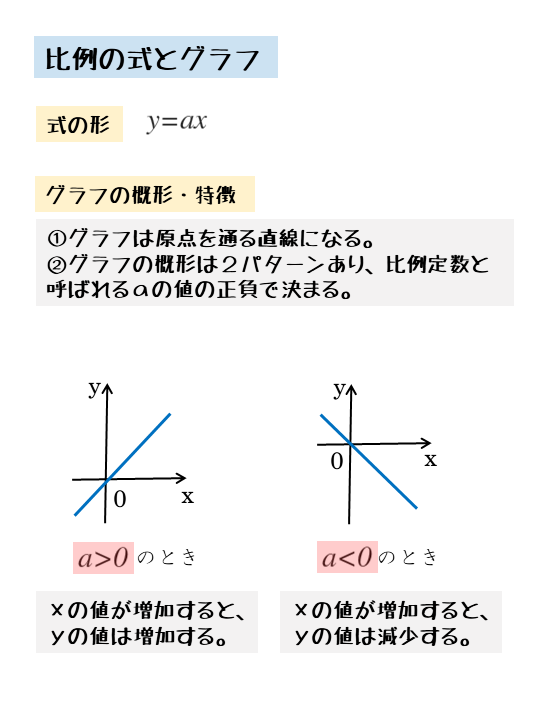



2次関数 関数について 日々是鍛錬 ひびこれたんれん




中1数学 直線の式の求め方 練習編1 映像授業のtry It トライイット




比例 と 反比例 の 利用 中学生必見 数学の無料プリント 復習用に 比例と反比例 Amp Petmd Com




書き方 反比例の双曲線グラフを5秒でかきおえる方法 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿